Zadanie nr 5712172
Dany jest trapez prostokątny 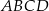 o podstawach
o podstawach 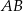 i
i 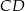 oraz wysokości
oraz wysokości 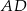 . Dwusieczna kąta
. Dwusieczna kąta 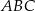 przecina ramię
przecina ramię 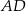 w punkcie
w punkcie 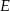 oraz dwusieczną kąta
oraz dwusieczną kąta 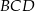 w punkcie
w punkcie 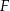 (zobacz rysunek).
(zobacz rysunek).
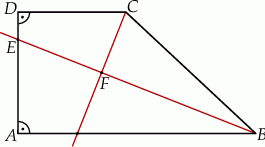
Wykaż, że w czworokącie 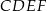 sumy miar przeciwległych kątów są sobie równe.
sumy miar przeciwległych kątów są sobie równe.
Rozwiązanie
Oznaczmy 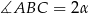 i
i 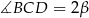 .
.
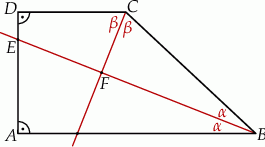
Zauważmy, że
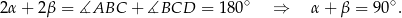
Stąd
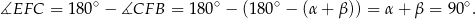
Mamy zatem
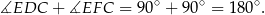
Suma dwóch pozostałych kątów czworokąta 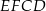 też jest równa
też jest równa 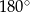 , bo suma wszystkich kątów czworokąta jest równa
, bo suma wszystkich kątów czworokąta jest równa 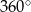 . Zatem rzeczywiście
. Zatem rzeczywiście