/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5720898

Dodaj do ulubionych
Dodaj do rozwiązanych

Znaleźć kąt ostry rombu, jeżeli wiadomo, że jego pole jest równe 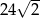√ -- 24 2 , a promień okręgu w niego wpisanego równy √ -- 6 .

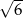Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

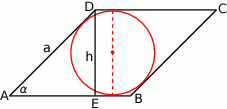
Zauważmy, że średnica okręgu wpisanego w romb ma długość równą odległości podstaw rombu, czyli długości jego wysokości. Zatem

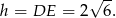
√ -- h = DE = 2 6.

Ponieważ znamy wysokość i pole rombu możemy obliczyć długość a jego podstawy.

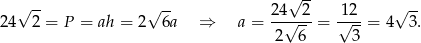
√ -- √ -- √ -- 24 2 12 √ -- 24 2 = P = ah = 2 6a ⇒ a = --√---= √---= 4 3. 2 6 3

Sposób I

Patrzymy na trójkąt prostokątny 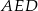AED .

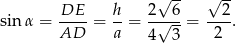
√ -- √ -- DE h 2 6 2 sinα = AD--= a-= -√---= -2-. 4 3

Zatem 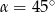∘ α = 4 5 .

Sposób II

Korzystamy ze wzoru na pole rombu z sinusem.

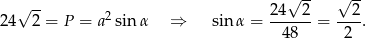
√ -- √ -- √ -- 24 2 2 24 2 = P = a2 sin α ⇒ sinα = ------= ---. 4 8 2

Zatem 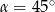∘ α = 4 5 .  
Odpowiedź: ∘ 45

Wersja PDF