Zadanie nr 5784895
Długości boków prostokąta są równe 3 oraz 5. Oblicz sinus kąta ostrego, który tworzą przekątne tego prostokąta.
Rozwiązanie
Szkicujemy prostokąt.
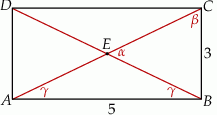
Korzystając z twierdzenia Pitagorasa obliczamy długość przekątnej prostokąta.
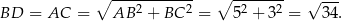
Sposób I
Skorzystamy z twierdzenia sinusów w trójkącie 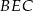 . Zanim jednak to zrobimy obliczamy
. Zanim jednak to zrobimy obliczamy 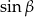 .
.
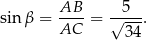
Zapisujemy teraz twierdzenie sinusów.
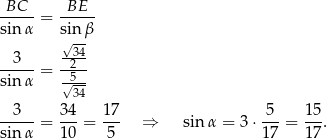
Sposób II
Interesujący nas sinus kąta między przekątnymi możemy obliczyć korzystając ze wzoru na pole trójkąta z sinusem.
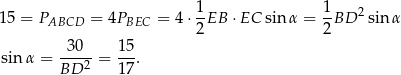
Sposób III
Tym razem skorzystamy z tego, że
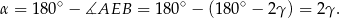
Mamy zatem
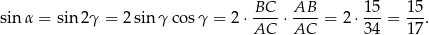
Odpowiedź: