/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5923764

Dodaj do ulubionych
Dodaj do rozwiązanych

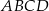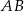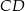Trapez prostokątny ABCD o podstawach AB i CD jest opisany na okręgu. Ramię 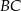BC ma długość 10, a ramię 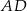AD jest wysokością trapezu. Podstawa 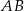AB jest 2 razy dłuższa od podstawy 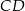CD . Oblicz pole tego trapezu.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

PIC

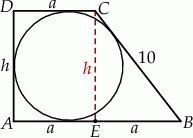
Korzystamy z faktu, że trapez jest opisany na okręgu. Oznacza to, że sumy przeciwległych boków są równe (ta własność w pełni charakteryzuje czworokąty opisane na okręgu, co warto zapamiętać). Zatem

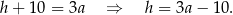
h + 10 = 3a ⇒ h = 3a − 10.

Piszemy teraz twierdzenie Pitagorasa w trójkącie CEB .

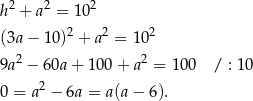
h 2 + a 2 = 102 2 2 2 (3a − 1 0) + a = 10 9a 2 − 6 0a+ 100 + a2 = 100 / : 10 0 = a2 − 6a = a(a − 6).

Stąd 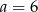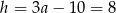a = 6 , h = 3a − 10 = 8 i pole trapezu jest równe

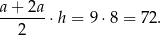
a+--2a-⋅h = 9 ⋅8 = 7 2. 2

 
Odpowiedź: 72

Wersja PDF