Zadanie nr 5933763
Podstawy trapezu mają długości  i
i 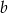 (
(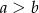 ). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi
). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi 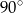 . Oblicz długość odcinka łączącego środki podstaw trapezu.
. Oblicz długość odcinka łączącego środki podstaw trapezu.
Rozwiązanie
Sposób I
Ponieważ suma kątów przy dłuższej podstawie jest równa 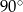 , każdy z tych kątów jest ostry, czyli możemy przedłużyć ramiona trapezu tak, aby przecięły się w pewnym punkcie
, każdy z tych kątów jest ostry, czyli możemy przedłużyć ramiona trapezu tak, aby przecięły się w pewnym punkcie 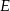 – rysunek.
– rysunek.
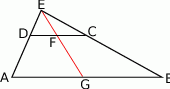
Jeżeli poprowadzimy w otrzymanym trójkącie środkową 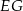 , to dzieli ona odcinek
, to dzieli ona odcinek 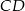 na połowy (twierdzenie Talesa). W takim razie odcinek, który mamy wyliczyć, to różnica środkowych
na połowy (twierdzenie Talesa). W takim razie odcinek, który mamy wyliczyć, to różnica środkowych 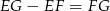 w trójkątach
w trójkątach 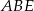 i
i 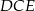 .
.
Pozostało skorzystać z podanego warunku 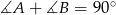 , czyli
, czyli 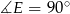 . Ponieważ środek okręgu opisanego na trójkącie prostokątnym to środek przeciwprostokątnej, to długość środkowej w trójkącie prostokątnym to połowa przeciwprostokątnej (bo jest to dokładnie promień okręgu opisanego). Mamy więc już wszystkie dane, aby wyliczyć szukaną długość odcinka
. Ponieważ środek okręgu opisanego na trójkącie prostokątnym to środek przeciwprostokątnej, to długość środkowej w trójkącie prostokątnym to połowa przeciwprostokątnej (bo jest to dokładnie promień okręgu opisanego). Mamy więc już wszystkie dane, aby wyliczyć szukaną długość odcinka 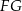 :
:
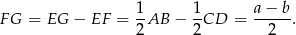
Sposób II
Dorysujmy odcinki równoległe do szukanego odcinka, ale przechodzące przez wierzchołki krótszej podstawy.
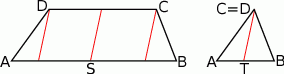
Jeżeli narysujemy dwa powstałe trójkąty obok siebie (tak by miały wspólny bok 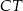 ), to otrzymany trójkąt
), to otrzymany trójkąt 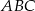 jest prostokątny (bo
jest prostokątny (bo 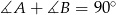 ). Ponadto jego przeciwprostokątna ma długośc równą różnicy między długościami podstaw trapezu, czyli
). Ponadto jego przeciwprostokątna ma długośc równą różnicy między długościami podstaw trapezu, czyli 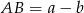 . Ponieważ punkt
. Ponieważ punkt 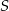 dzielił podstawę trapezu na połowy, to odpowiadający punkt
dzielił podstawę trapezu na połowy, to odpowiadający punkt 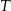 w trójkącie
w trójkącie 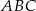 jest środkiem boku
jest środkiem boku 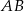 . Pozostało, jak w poprzednim sposobie, zauważyć, że środkowa
. Pozostało, jak w poprzednim sposobie, zauważyć, że środkowa 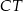 w trójkącie prostokątnym ma długość równą połowie długości przeciwprostokątnej, czyli
w trójkącie prostokątnym ma długość równą połowie długości przeciwprostokątnej, czyli 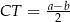 .
.
Odpowiedź: