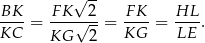Zadanie nr 5974568
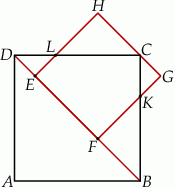
Bok 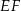 kwadratu
kwadratu 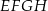 zawiera się w przekątnej
zawiera się w przekątnej 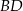 kwadratu
kwadratu 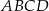 , a punkt
, a punkt 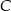 należy do odcinka
należy do odcinka 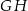 . Odcinki
. Odcinki 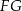 i
i 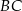 przecinają się w punkcie
przecinają się w punkcie 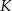 , a odcinki
, a odcinki 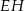 i
i 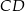 przecinają się w punkcie
przecinają się w punkcie 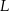 . Wykaż, że
. Wykaż, że 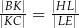 .
.
Rozwiązanie
Zauważmy, że każdy z trójkątów 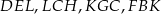 jest prostokątny i równoramienny (kąty ostre każdego z tych trójkątów mają miarę
jest prostokątny i równoramienny (kąty ostre każdego z tych trójkątów mają miarę 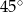 ). Ponadto
). Ponadto
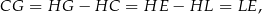
więc trójkąty 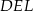 i
i 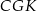 są przystające. Podobnie uzasadniamy, że trójkąty
są przystające. Podobnie uzasadniamy, że trójkąty 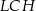 i
i 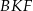 są przystające:
są przystające:
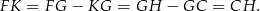
Sposób I
Korzystając z podobieństwa trójkątów 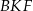 i
i 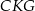 mamy
mamy
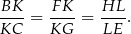
Sposób II
Ponieważ 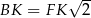 oraz
oraz 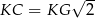 mamy
mamy