Zadanie nr 6082140
Przekątne rombu mają długość 8 cm i 13 cm. Oblicz pole czworokąta, którego wierzchołkami są środki boków romb.
Rozwiązanie
Zaczynamy od rysunku
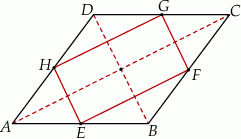
Zauważmy, że odcinek 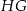 łączy środki boków w trójkącie
łączy środki boków w trójkącie 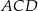 . Zatem jest on równoległy do przekątnej
. Zatem jest on równoległy do przekątnej 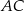 oraz
oraz
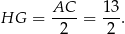
Analogicznie (patrząc na trójkąty 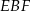 i
i 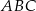 ) uzasadniamy, że odcinek
) uzasadniamy, że odcinek 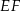 jest równoległy do
jest równoległy do 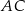 oraz
oraz
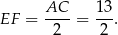
Podobnie uzasadniamy, że każdy z odcinków 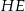 i
i 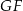 jest równoległy do
jest równoległy do 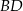 oraz
oraz
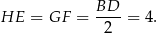
Ponieważ przekątne rombu są prostopadłe, czworokąt 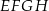 jest prostokątem i jego pole jest równe
jest prostokątem i jego pole jest równe
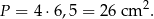
Odpowiedź: