Zadanie nr 6104929
W trapezie równoramiennym 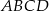 , w którym
, w którym 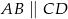 , dane są
, dane są 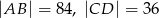 ,
, 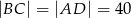 . Oblicz promień okręgu wpisanego w trójkąt
. Oblicz promień okręgu wpisanego w trójkąt 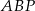 , gdzie
, gdzie 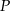 jest punktem przecięcia przekątnych tego trapezu.
jest punktem przecięcia przekątnych tego trapezu.
Rozwiązanie
Szkicujemy opisaną sytuację.
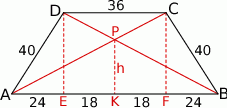
Niech 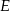 i
i 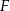 będą spodkami wysokości trapezu opuszczonych z wierzchołków
będą spodkami wysokości trapezu opuszczonych z wierzchołków 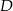 i
i 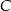 , a
, a 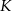 niech będzie rzutem punktu
niech będzie rzutem punktu 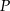 na prostą
na prostą 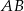 . Mamy wtedy
. Mamy wtedy
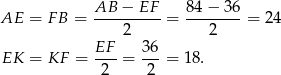
Z trójkąta prostokątnego 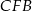 obliczamy wysokość trapezu
obliczamy wysokość trapezu
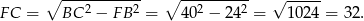
Z trójkąta prostokątnego 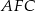 obliczamy długość przekątnej trapezu.
obliczamy długość przekątnej trapezu.
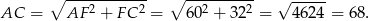
Zauważmy teraz, że trójkąty prostokątne 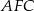 i
i 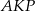 mają wspólny kąt ostry, więc są podobne. Mamy stąd
mają wspólny kąt ostry, więc są podobne. Mamy stąd
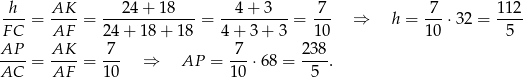
Pozostało teraz obliczyć promień okręgu wpisanego w trójkąt 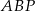 – korzystamy ze wzoru na pole
– korzystamy ze wzoru na pole 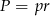 , gdzie
, gdzie 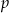 jest połową obwodu trójkąta. Mamy więc
jest połową obwodu trójkąta. Mamy więc
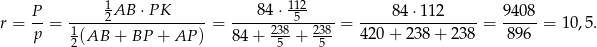
Odpowiedź: 10,5

