/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 6123191

Dodaj do ulubionych
Dodaj do rozwiązanych

W kwadrat wpisano drugi kwadrat, którego wierzchołki leżą na bokach pierwszego i boki tworzą z bokami pierwszego kwadratu kąty o miarach 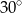3 0∘ . Jaką częścią pola dużego kwadratu jest pole małego kwadratu?

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

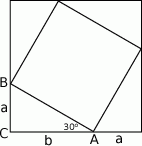
Sposób I

Z trójkąta 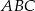ABC mamy

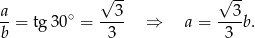
√ -- √ -- a-= tg 30∘ = --3- ⇒ a = --3-b. b 3 3

Szukany stosunek pól kwadratów jest więc równy

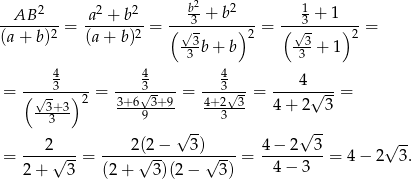
2 --AB-2-- a2-+-b2- ---b3-+-b2--- ---13-+-1--- (a+ b)2 = (a + b )2 = ( √3 ) 2 = ( √ 3 )2 = -3 b + b -3-+ 1 4 4 4 ----3---- ---3----- --3--- ----4---- = ( √3+ 3)2 = 3+6√-3+-9 = 4+2√-3= 4 + 2√ 3 = --3-- 9 3 √ -- √ -- -- = ---2√---= ----2(√2-−---3)√----= 4−--2--3-= 4 − 2√ 3 . 2 + 3 (2+ 3)(2 − 3) 4 − 3

Sposób II

Rachunki będą odrobinę prostsze jeżeli wyznaczmy 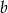b w zależności od a .

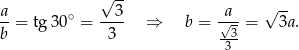
√ -- a ∘ 3 a √ -- --= tg 30 = ---- ⇒ b = -√3 = 3a. b 3 3--

Szukany stosunek pól jest równy

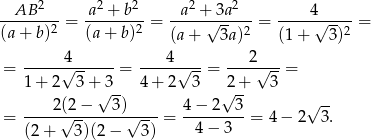
2 2 2 2 2 --AB---- = -a-+--b- = -a--+√3a----= ----4√-----= (a+ b)2 (a + b)2 (a+ 3a)2 (1+ 3)2 = -----4√-------= ---4-√---= ---2√---= 1+ 2 3 + 3 4+ 2 3 2+ 3 √ -- √ -- √ -- = ----2(√2-−---3)√----= 4−--2--3-= 4 − 2 3. (2+ 3)(2 − 3) 4 − 3

 
Odpowiedź: √ -- 4 − 2 3

Wersja PDF