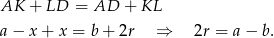/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 6136387

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku wpisano dwa przystające okręgi styczne zewnętrznie do siebie (patrz rysunek). Wykaż, że średnica każdego z tych okręgów jest równa różnicy długości dłuższego i krótszego boku tego równoległoboku.

PIC

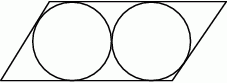
Rozwiązanie

Sposób I

Połączmy środki okręgów z punktami styczności.

PIC

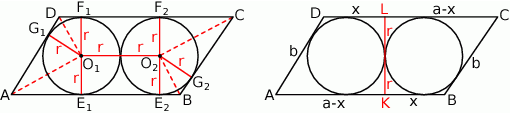
Zauważmy, że zarówno trójkąty

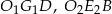
O G D , O E B 1 1 2 2

jak i

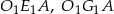
O E A , O G A 1 1 1 1

są przystające. To oznacza, że

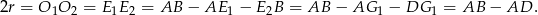
2r = O1O 2 = E 1E 2 = AB − AE 1 − E 2B = AB − AG 1 − DG 1 = AB − AD .

Sposób II

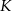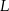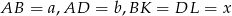Poprowadźmy trzecią wspólną styczną do danych okręgów i oznaczmy przez K i L punkty wspólne tej stycznej z bokami równoległoboku. Oznaczmy ponadto AB = a,AD = b,BK = DL = x .

Ponieważ czworokąt 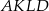AKLD jest opisany na okręgu, mamy

AK + LD = AD + KL a − x + x = b+ 2r ⇒ 2r = a − b.
Wersja PDF