Zadanie nr 6475298
Punkty 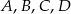 są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku
są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku 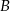 ma miarę
ma miarę 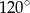 i promień okręgu wpisanego w trójkąt
i promień okręgu wpisanego w trójkąt 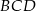 jest równy
jest równy 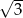 , oblicz długości boków i pole tego równoległoboku.
, oblicz długości boków i pole tego równoległoboku.
Rozwiązanie
Zacznijmy od rysunku i oznaczmy boki równoległoboku przez  i
i 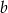 .
.
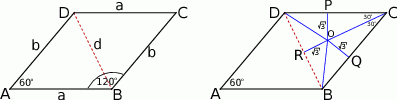
Sposób I
Wiemy, że
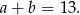
Aby wyliczyć  i
i 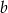 potrzebujemy jeszcze jednego równania – otrzymamy je z podanej długości promienia okręgu wpisanego w trójkąt
potrzebujemy jeszcze jednego równania – otrzymamy je z podanej długości promienia okręgu wpisanego w trójkąt 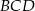 (lub
(lub 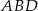 , bo trójkąty te są przystające). Jedyny sposób na wyliczenie promienia okręgu wpisanego to wzór na pole
, bo trójkąty te są przystające). Jedyny sposób na wyliczenie promienia okręgu wpisanego to wzór na pole
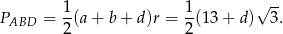
Pole wyliczamy ze wzoru z sinusem
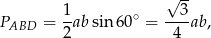
a długość 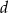 przekątnej wyliczamy z twierdzenia cosinusów.
przekątnej wyliczamy z twierdzenia cosinusów.
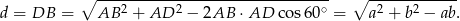
Mamy zatem
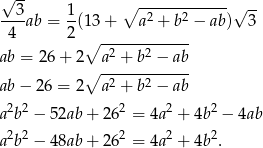
Korzystamy teraz z równości 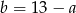 i
i 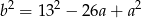
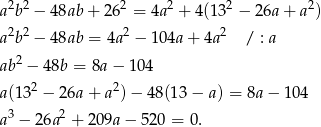
Szukając całkowitych pierwiastków można sprawdzić, że 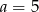 jest pierwiastkiem. Dzielimy wielomian przez
jest pierwiastkiem. Dzielimy wielomian przez 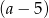 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
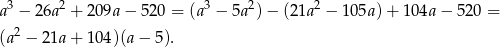
Rozkładamy wielomian w nawiasie, 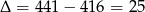 . Stąd
. Stąd 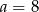 lub
lub 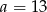 . Ponieważ jednak
. Ponieważ jednak 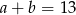 , drugi z pierwiastków odrzucamy. Zatem
, drugi z pierwiastków odrzucamy. Zatem 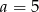 i
i 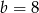 lub
lub 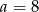 i
i 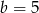 .
.
Pozostało policzyć pole
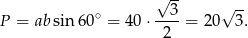
Sposób II
W zasadzie jest to uproszczenie poprzedniego sposobu. Jak poprzednio dochodzimy do równości
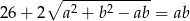
Teraz jednak zauważmy, że
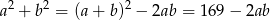
Tak więc
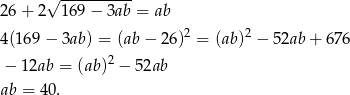
Mamy zatem układ równań
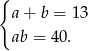
Na mocy wzorów Viéte’a, rozwiązaniami tego układu są pierwiastki równania
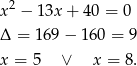
Zatem boki równoległoboku mają długości 5 i 8. Pole liczymy jak poprzednio.
Sposób III
Tym razem zróbmy trochę dokładniejszy rysunek: połączmy środek 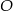 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 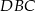 z jego wierzchołkami, oraz z z jego rzutami
z jego wierzchołkami, oraz z z jego rzutami 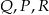 na boki
na boki 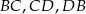 . Otrzymujemy w ten sposób trzy pary przystających trójkątów prostokątnych, więc
. Otrzymujemy w ten sposób trzy pary przystających trójkątów prostokątnych, więc 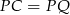 ,
, 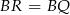 and
and 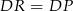 . Patrząc na trójkąt
. Patrząc na trójkąt 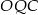 mamy
mamy
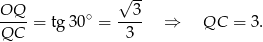
Zatem
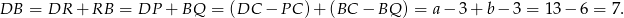
Piszemy teraz twierdzenie cosinusów w trójkącie 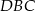 .
.
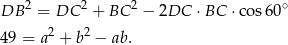
Korzystamy teraz z równości 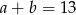 .
.
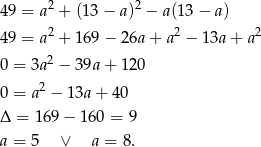
Zatem boki mają długości 5 i 8. Pole liczymy jak w poprzednim sposobie.
Odpowiedź: Boki: 5 i 8, pole: