/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 6506933

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątne rombu 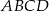ABCD , o kącie ostrym przy wierzchołku 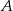A , mają długości 6cm i 8cm.

  • Oblicz cosinus kąta CAD .
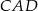  • Wyznacz promień okręgu wpisanego w romb.

Rozwiązanie

Zacznijmy od rysunku.

PIC

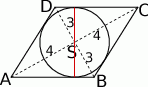
  • Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, to trójkąt 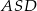ASD jest trójkątem prostokątnym o przyprostokątnych długości 3 i 4. Zatem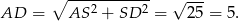
    ∘ ------------ √ --- AD = AS 2 + SD 2 = 25 = 5.

    Stąd

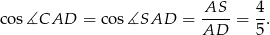
    AS 4 cos ∡CAD = cos ∡SAD = ----= -. AD 5

     
    Odpowiedź: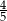 45

  • Promień okręgu wpisanego w romb to dokładnie połowa jego wysokości. Wysokość tę możemy wyliczyć ze wzoru na pole. Pole rombu jest 4 razy większe od pola trójkąta 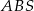ABS , jest więc równe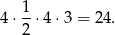
    4⋅ 1⋅ 4⋅3 = 24. 2

    Zatem wysokość

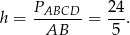
    PABCD 2 4 h = ------- = ---. AB 5

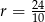    Szukany promień to połowa wysokości, czyli r = 2140 .  
    Odpowiedź: 24 10

Wersja PDF