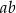/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 6646131

Dodaj do ulubionych
Dodaj do rozwiązanych

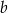Trapez prostokątny o podstawach a i b jest opisany na okręgu. Oblicz pole tego trapezu.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

PIC

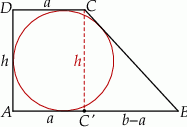
Aby obliczyć pole trapezu, musimy wyznaczyć jego wysokość 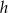h . Na mocy twierdzenia Pitagorasa zastosowanego do trójkąta 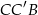CC ′B mamy

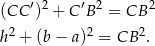
(CC ′)2 + C′B 2 = CB 2 2 2 2 h + (b − a) = CB .

Ponadto, musimy w końcu wykorzystać fakt, że trapez jest opisany na okręgu. Oznacza to, że sumy przeciwległych boków są równe (ta własność w pełni charakteryzuje czworokąty opisane na okręgu, co warto zapamiętać). Zatem

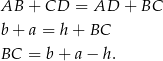
AB + CD = AD + BC b+ a = h + BC BC = b + a− h.

Podstawiamy tę wartość do wcześniej napisanego twierdzenia Pitagorasa i otrzymujemy

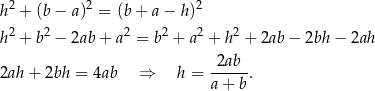
h2 + (b − a)2 = (b + a − h)2 h2 + b2 − 2ab + a2 = b2 + a2 + h2 + 2ab − 2bh − 2ah 2ab 2ah + 2bh = 4ab ⇒ h = -----. a + b

Możemy więc obliczyć pole

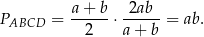
PABCD = a+--b⋅ -2ab--= ab. 2 a+ b

 
Odpowiedź: ab

Wersja PDF