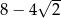Zadanie nr 6698959
Dwa kwadraty 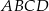 i
i 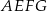 o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta
o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta 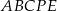 .
.
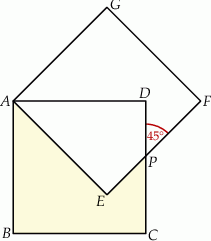
Rozwiązanie
Sposób I
Interesujący nas pięciokąt składa się z dwóch równoramiennych trójkątów prostokątnych: 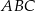 i
i 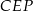 .
.
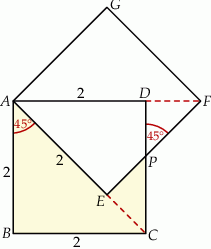
Ponadto, 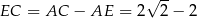 . W takim razie
. W takim razie
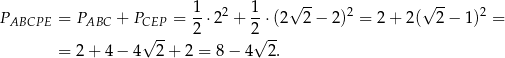
Sposób II
Tym razem obliczmy najpierw pole czworokąta 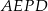 .
.
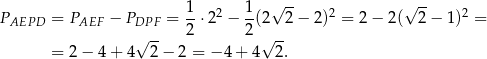
Stąd
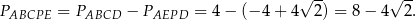
Odpowiedź: