/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 6742609

Dodaj do ulubionych
Dodaj do rozwiązanych

W romb o boku równym 8 i kącie ostrym równym 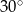∘ 30 wpisano koło, a następnie w to koło wpisano kwadrat. Wyznacz stosunek pola rombu do pola kwadratu.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

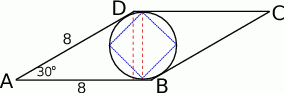
Średnica okręgu wpisanego w romb to dokładnie wysokość rombu, zatem

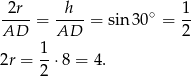
-2r- = --h- = sin 30∘ = 1- AD AD 2 1 2r = --⋅8 = 4. 2

Ta średnica to dokładnie przekątna kwadratu wpisanego w to koło, czyli

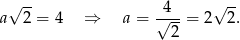
√ -- 4 √ -- a 2 = 4 ⇒ a = √---= 2 2. 2

Zatem pole kwadratu jest równe

Pk = 8

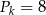
Tymczasem pole rombu jest równe

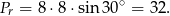
∘ Pr = 8 ⋅8 ⋅sin30 = 32.

Szukany stosunek wynosi więc

32 ---= 4 8

 
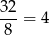
Odpowiedź: 4

Wersja PDF