Zadanie nr 7079488
Boki prostokąta 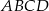 mają długości
mają długości 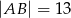 i
i 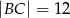 . Punkt
. Punkt 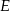 jest punktem boku
jest punktem boku 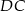 takim, że
takim, że 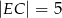 , a punkt
, a punkt 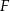 jest takim punktem odcinka
jest takim punktem odcinka 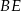 , że
, że 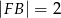 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 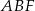 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
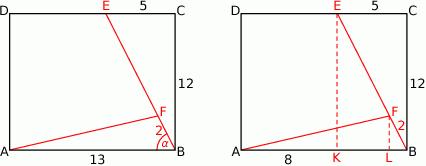
Sposób I
Promień okręgu opisanego na trójkącie 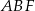 możemy obliczyć stosując twierdzenie sinusów, ale do tego potrzebujemy znać długość boku trójkąta oraz sinus kąta leżącego naprzeciwko tego boku. Dość łatwo jest obliczyć
możemy obliczyć stosując twierdzenie sinusów, ale do tego potrzebujemy znać długość boku trójkąta oraz sinus kąta leżącego naprzeciwko tego boku. Dość łatwo jest obliczyć 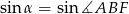 , więc od tego zaczniemy. Od razu obliczymy też
, więc od tego zaczniemy. Od razu obliczymy też 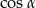 , bo przyda nam się do obliczenia długości odcinka
, bo przyda nam się do obliczenia długości odcinka 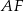 (z twierdzenia cosinusów).
(z twierdzenia cosinusów).
Na mocy twierdzenia Pitagorasa
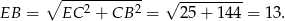
Stąd
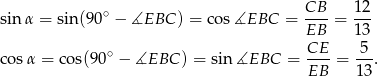
Przy pomocy twierdzenia cosinusów obliczamy teraz długość odcinka 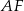 .
.
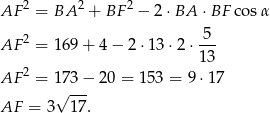
Pozostało skorzystać z twierdzenia sinusów.
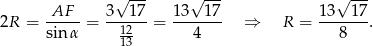
Sposób II
Tym razem obliczymy pole i wszystkie boki trójkąta 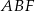 , aby móc skorzystać ze wzoru na pole
, aby móc skorzystać ze wzoru na pole 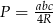 .
.
Zauważmy najpierw, że
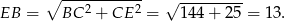
Niech 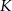 i
i 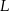 będą rzutami punktów
będą rzutami punktów 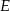 i
i 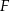 na prostą
na prostą 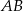 . Z podobieństwa trójkątów
. Z podobieństwa trójkątów 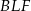 i
i 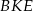 mamy
mamy
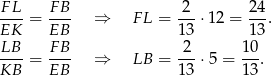
Teraz możemy obliczyć pole trójkąta 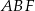 .
.
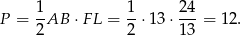
Długość odcinka 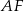 obliczamy z trójkąta prostokątnego
obliczamy z trójkąta prostokątnego 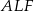 .
.
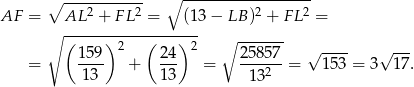
Pozostało skorzystać ze wzoru na pole 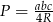 .
.
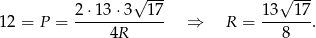
Odpowiedź: