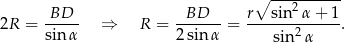/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7196772

Dodaj do ulubionych
Dodaj do rozwiązanych

Na okręgu o promieniu r opisano trapez równoramienny, którego kąt ostry ma miarę α . Wykaż, że promień okręgu opisanego na tym czworokącie jest równy 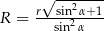√ ------- r--sin2α+-1 R = sin2α .

Rozwiązanie

Zaczynamy od rysunku.

PIC

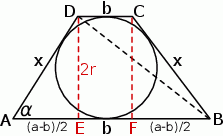
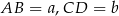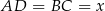Jeżeli oznaczymy AB = a,CD = b i AD = BC = x , to ponieważ czworokąt 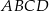ABCD jest opisany na okręgu, mamy

a + b = 2x.

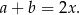
Ponadto

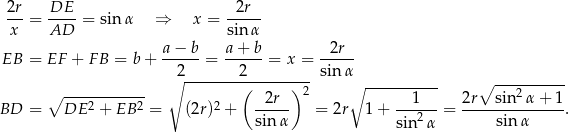
2r-= DE--= sin α ⇒ x = -2r-- x AD sin α a − b a + b 2r EB = EF + F B = b + --2---= --2---= x = sinα- ∘ --------(------)-- ∘ ---------- ∘ ---------- ∘ ------------ 2r 2 1 2r sin2α + 1 BD = DE 2 + EB 2 = (2r)2 + ----- = 2r 1 + ---2-- = --------------. sinα sin α sin α

Pozostało skorzystać z twierdzenia sinusów w trójkącie 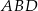ABD .

∘ ---------- BD BD r sin2 α+ 1 2R = ----- ⇒ R = -------= -------2-----. sin α 2 sinα sin α
Wersja PDF