/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7218513

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątne rombu 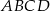ABCD przecinają się w punkcie 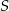S . Punkt 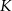K jest takim punktem boku 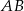AB , że odcinek 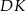DK jest wysokością rombu (zobacz rysunek).

PIC

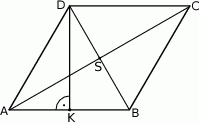
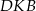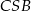Wykaż, że jeżeli trójkąty DKB i CSB są przystające, to punkt 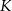K jest środkiem odcinka AB .

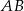Rozwiązanie

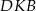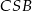Zauważmy najpierw, że trójkąty DKB i CSB są podobne. Rzeczywiście, oba są prostokątne (bo przekątne rombu są prostopadłe) oraz mają taki sam kąt ostry

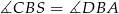
∡CBS = ∡DBA

(bo przekątne rombu są dwusiecznymi jego kątów wewnętrznych). Jeżeli trójkąty te są przystające, to ich przeciwprostokątne mają tę samą długość, więc

BD = BC ,

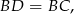
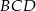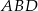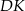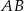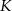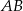a to oznacza, że trójkąt BCD jest równoboczny. Równoboczny jest więc też trójkąt ABD , więc jego wysokość DK jest jednocześnie symetralną odcinka AB . To dowodzi, że K jest środkiem odcinka AB .

Wersja PDF