Zadanie nr 7225567
Czworokąt 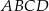 jest wpisany w okrąg o promieniu
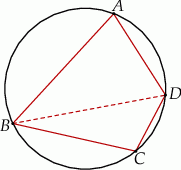
jest wpisany w okrąg o promieniu 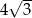 (patrz rysunek). Przekątna
(patrz rysunek). Przekątna 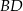 czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy
czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy 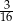 . Wiedząc, że
. Wiedząc, że 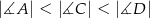 , oblicz miary kątów czworokąta
, oblicz miary kątów czworokąta 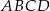 .
.
Rozwiązanie
Na mocy twierdzenia sinusów w trójkącie 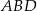 mamy
mamy
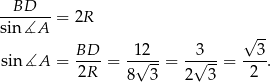
Zatem 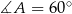 lub
lub 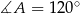 . Ponieważ jednak
. Ponieważ jednak 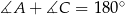 (własność czworokąta wpisanego w okrąg) i
(własność czworokąta wpisanego w okrąg) i 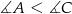 musimy mieć
musimy mieć 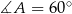 i
i 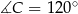 .
.
Zapiszmy teraz warunek z iloczynem sinusów
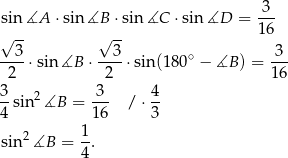
Ponieważ sinus jest dodatni w pierwszych dwóch ćwiartkach, mamy stąd 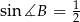 . Zatem
. Zatem 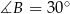 lub
lub 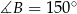 . Ponieważ jednak
. Ponieważ jednak 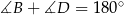 i
i 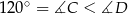 musimy mieć
musimy mieć 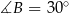 i
i 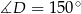 .
.
Odpowiedź: