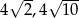/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7255516

Dodaj do ulubionych
Dodaj do rozwiązanych

Kąt ostry równoległoboku ma miarę 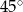∘ 45 . Punkt wspólny przekątnych równoległoboku jest oddalony od boków o 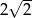√ -- 2 2 i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.

Rozwiązanie

Zaczynamy od rysunku.

PIC

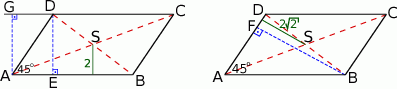
Ponieważ przekątne równoległoboku dzielą się na połowy, z twierdzenia Talesa, odległości punktu przecięcia się przekątnych od boków równoległoboku są równe połowie odpowiednich wysokości. Zatem 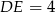DE = 4 i z trójkąta 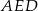AED możemy wyliczyć długości odcinków 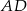AD i AE .

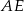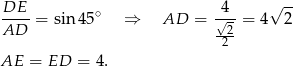
DE 4 √ -- ---- = sin 45∘ ⇒ AD = -√- = 4 2 AD 22- AE = ED = 4.

Podobnie wyliczamy długość drugiego boku.

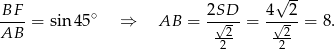
√ -- BF--= sin45 ∘ ⇒ AB = 2S√D-- = 4√--2 = 8. AB --2 --2 2 2

Mamy zatem pole

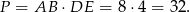
P = AB ⋅ DE = 8 ⋅4 = 32.

oraz przekątne

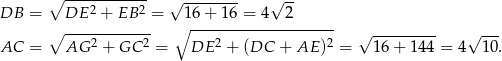
∘ ---2------2- √ -------- √ -- DB = DE + EB = ∘ 16-+-16-=-4---2------ ∘ ---2------2- 2 2 √ --------- √ --- AC = AG + GC = DE + (DC + AE ) = 16+ 144 = 4 1 0.

 
Odpowiedź: 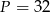P = 32 , przekątne: √ -- √ --- 4 2,4 10

Wersja PDF