/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7262260

Dodaj do ulubionych
Dodaj do rozwiązanych

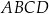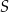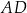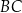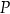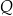W trapez ABCD wpisano okrąg o środku S . Okrąg ten jest styczny do ramion AD i BC tego trapezu w punktach odpowiednio P i Q (zobacz rysunek).

PIC

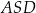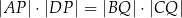Uzasadnij, że trójkąt ASD jest prostokątny. Wykaż, że |AP |⋅|DP | = |BQ | ⋅|CQ | .

Rozwiązanie

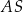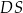Odcinki AS i DS są fragmentami dwusiecznych kątów wewnętrznych trapezu, więc

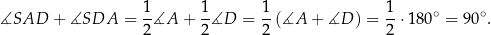
∡SAD + ∡SDA = 1∡A + 1∡D = 1-(∡A + ∡D ) = 1-⋅18 0∘ = 90∘. 2 2 2 2

To oczywiście oznacza, że 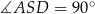∡ASD = 90∘ i trójkąt 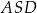ASD jest prostokątny. Analogicznie uzasadniamy, że trójkąt 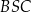BSC jest prostokątny.

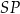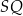Dorysujmy teraz promienie SP i SQ – zauważmy, że są to wysokości w trójkątach prostokątnych 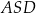ASD i BSC .

PIC

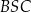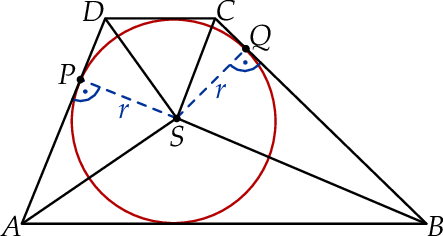
Chcemy teraz skorzystać z faktu, że wysokość opuszczona z wierzchołka kąta prostego w trójkącie prostokątnym jest średnią geometryczną długości odcinków, na które ta wysokość dzieli przeciwprostokątną. Fakt ten łatwo uzasadnić – wystarczy skorzystać z podobieństwa trójkątów prostokątnych 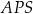AP S i SP D .

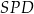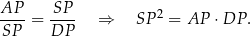
AP SP ----= ---- ⇒ SP2 = AP ⋅DP . SP DP

Mamy zatem

2 2 AP ⋅ DP = SP = SQ = BQ ⋅CQ .
Wersja PDF