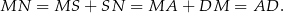Zadanie nr 7305448
Dany jest prostokąt 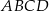 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 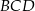 jest styczny do przekątnej
jest styczny do przekątnej 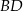 w punkcie
w punkcie 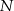 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 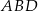 jest styczny do boku
jest styczny do boku 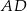 w punkcie
w punkcie 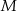 , a środek
, a środek 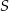 tego okręgu leży na odcinku
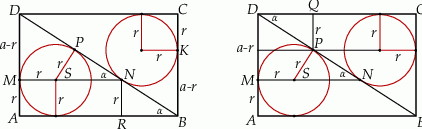
tego okręgu leży na odcinku 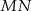 , jak na rysunku.
, jak na rysunku.
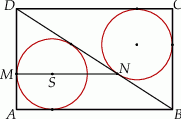
Wykaż, że 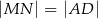 .
.
Rozwiązanie
Sposób I
Niech 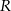 będzie rzutem punktu
będzie rzutem punktu 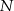 na bok
na bok 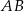 , a
, a 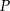 niech będzie rzutem
niech będzie rzutem 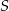 na przekątną
na przekątną 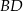 .
.
Trójkąty 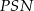 i
i 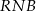 są prostokątne oraz mają wspólny kąt
są prostokątne oraz mają wspólny kąt
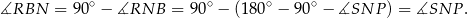
Ponadto w obu trójkątach przyprostokątne leżące naprzeciw tych kątów mają tę samą długość  . To oznacza, że trójkąty
. To oznacza, że trójkąty 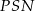 i
i 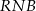 są przystające. W szczególności
są przystające. W szczególności
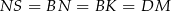
(skorzystaliśmy z tego, że odcinki stycznych do okręgu poprowadzonych z punktu 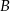 maję tę samą długość). Mamy zatem
maję tę samą długość). Mamy zatem
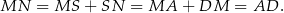
Sposób II
Tak samo jak poprzednio niech 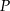 będzie rzutem punktu
będzie rzutem punktu 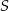 na przekątną
na przekątną 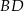 . Zauważmy, że środek prostokąta jest środkiem symetrii danego rysunku, więc punkt
. Zauważmy, że środek prostokąta jest środkiem symetrii danego rysunku, więc punkt 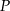 leży na prostej równoległej do
leży na prostej równoległej do 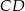 i przechodzącej przez środek okręgu wpisanego w trójkąt
i przechodzącej przez środek okręgu wpisanego w trójkąt 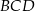 . Niech
. Niech 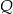 będzie rzutem punktu
będzie rzutem punktu 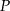 na bok
na bok 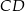 . Zauważmy, że trójkąty
. Zauważmy, że trójkąty 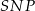 i
i 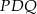 są prostokątne oraz mają wspólny kąt ostry
są prostokątne oraz mają wspólny kąt ostry
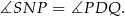
Ponadto w obu trójkątach przyprostokątne leżące naprzeciw tych kątów mają tę samą długość  . To oznacza, że trójkąty
. To oznacza, że trójkąty 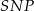 i
i 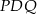 są przystające. W szczególności
są przystające. W szczególności
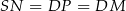
(skorzystaliśmy z tego, że odcinki stycznych do okręgu poprowadzonych z punktu 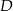 maję tę samą długość). Mamy zatem
maję tę samą długość). Mamy zatem