/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7338512

Dodaj do ulubionych
Dodaj do rozwiązanych

Sinus kąta jaki tworzą przekątne prostokąta o polu 60 jest równy 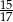15 17 . Oblicz obwód tego prostokąta.

Rozwiązanie

Oznaczmy długości boków prostokąta przez a i b .

PIC

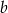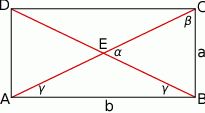
Korzystając z twierdzenia Pitagorasa obliczamy długość przekątnej prostokąta.

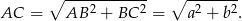
∘ ------------ ∘ ------- AC = AB 2 + BC 2 = a2 + b2.

Sposób I

Skorzystamy z twierdzenia sinusów w trójkącie 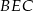BEC . Zanim jednak to zrobimy obliczamy sin β .

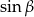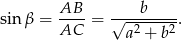
AB-- ----b---- sin β = AC = √ -2----2. a + b

Zapisujemy teraz twierdzenie sinusów.

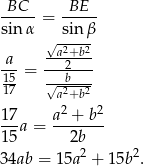
-BC-- BE--- sin α = sin β √ ----- a --a2+b-2 -15-= ---2b--- 17 √a-2+b-2 2 2 17-a = a--+-b- 15 2b 34ab = 15a2 + 15b2.

Aby dalej przekształcić tę równość korzystamy z podanego pola: 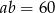ab = 60 .

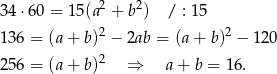
34 ⋅60 = 15 (a2 + b 2) / : 15 136 = (a+ b )2 − 2ab = (a+ b)2 − 120 2 256 = (a+ b ) ⇒ a+ b = 16.

Podstawiamy teraz 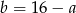b = 16 − a w równości ab = 60 .

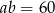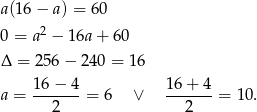
a (1 6− a) = 60 0 = a2 − 16a+ 60 Δ = 256 − 2 40 = 16 16-−-4- 16-+-4- a = 2 = 6 ∨ 2 = 10.

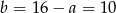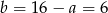Mamy wtedy odpowiednio b = 1 6− a = 10 i b = 1 6− a = 6 . Obwód prostokąta jest więc równy

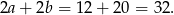
2a + 2b = 12+ 20 = 32.

Sposób II

Tym razem korzystamy ze wzoru na pole trójkąta z sinusem.

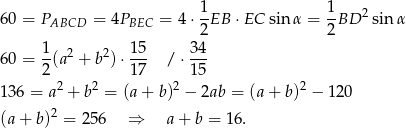
1 1 60 = PABCD = 4PBEC = 4⋅--EB ⋅EC sinα = -BD 2sinα 2 2 1- 2 2 15- 34- 60 = 2(a + b ) ⋅17 / ⋅15 2 2 2 2 13 6 = a + b = (a + b) − 2ab = (a + b) − 120 (a + b)2 = 2 56 ⇒ a + b = 16.

Dalej obliczenia prowadzimy tak samo jak w pierwszym sposobie.

Sposób III

Tym razem skorzystamy z tego, że

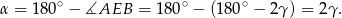
α = 180∘ − ∡AEB = 180∘ − (180 ∘ − 2 γ) = 2γ .

Mamy zatem

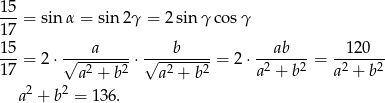
15- 17 = sin α = sin 2γ = 2 sin γ cos γ 15 a b ab 120 ---= 2 ⋅√-------- ⋅√-------- = 2⋅ ------- = ------- 17 a 2 + b2 a 2 + b2 a2 + b2 a2 + b2 a2 + b2 = 13 6.

Dalej liczymy tak samo jak w poprzednich sposobach.  
Odpowiedź: 32

Wersja PDF