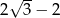/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7365765

Dodaj do ulubionych
Dodaj do rozwiązanych

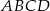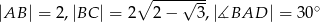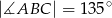W deltoidzie ABCD dane są ∘ ----√--- ∘ |AB | = 2 ,|BC | = 2 2− 3,|∡BAD | = 3 0 i |∡ABC | = 135∘ (zobacz rysunek). Oblicz pole tego deltoidu.

PIC

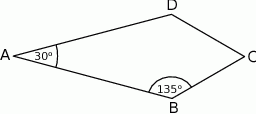
Rozwiązanie

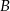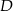Kąty B i D są przystające, więc

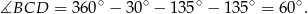
∘ ∘ ∘ ∘ ∘ ∡BCD = 360 − 30 − 135 − 1 35 = 60 .

W takim razie trójkąt 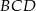BCD jest równoboczny i jego pole jest równe (korzystamy ze wzoru 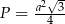2√ - P = a---3 4 na pole trójkąta równobocznego o boku a ).

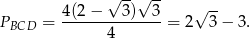
√ --√ -- 4 (2− 3) 3 √ -- PBCD = -------------- = 2 3 − 3. 4

Pole trójkąta 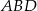ABD obliczamy ze wzoru z sinusem.

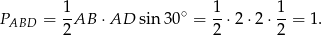
1- ∘ 1- 1- PABD = 2AB ⋅AD sin30 = 2 ⋅2 ⋅2⋅ 2 = 1.

Pole deltoidu jest więc równe

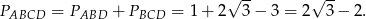
√ -- √ -- PABCD = PABD + PBCD = 1+ 2 3 − 3 = 2 3 − 2 .

 
Odpowiedź: √ -- 2 3 − 2

Wersja PDF