Zadanie nr 7466118
W trapez równoramienny o obwodzie 60 wpisano okrąg. Przekątna trapezu ma długość 17. Oblicz pole trapezu.
Rozwiązanie
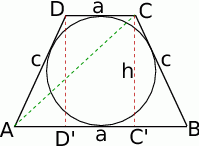
Zacznijmy od rysunku i oznaczmy krótszą podstawę trapezu przez  , ramię przez
, ramię przez  a wysokość przez
a wysokość przez 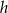 .
.
Ponieważ w trapez można wpisać okrąg, sumy długości przeciwległych boków są równe. Ponieważ obwód jest równy 60, to sumy te są równe po 30. W szczególności
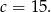
Na rysunku widzimy jak wysokości trapezu dzielą dłuższą podstawę na trzy odcinki, środkowy ma długość  , a dwa pozostałe będą mieć długość
, a dwa pozostałe będą mieć długość 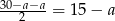 . W takim razie
. W takim razie 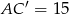 . Liczymy teraz wysokość
. Liczymy teraz wysokość 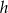 z trójkąta prostokątnego
z trójkąta prostokątnego 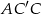 .
.
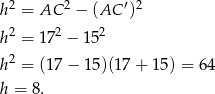
Możemy zatem policzyć pole
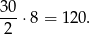
Odpowiedź: 120

