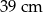Zadanie nr 7553290
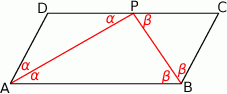
W równoległoboku 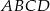 środek
środek 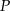 boku
boku 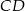 połączono odcinkami z wierzchołkami
połączono odcinkami z wierzchołkami 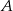 i
i 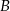 . Wiadomo, że
. Wiadomo, że 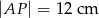 i
i 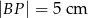 oraz
oraz 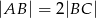 . Oblicz obwód równoległoboku.
. Oblicz obwód równoległoboku.
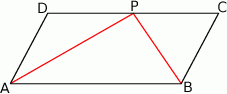
Rozwiązanie
Zauważmy, że
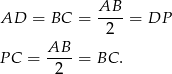
Zatem trójkąty 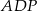 i
i 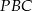 są równoramienne. Oznaczmy
są równoramienne. Oznaczmy 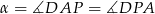 i
i 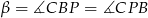 .
.
Proste 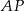 i
i 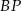 przecinają proste równoległe
przecinają proste równoległe 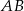 i
i 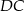 pod tym samym kątem, więc
pod tym samym kątem, więc
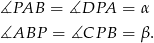
Mamy ponadto
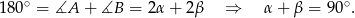
To z kolei oznacza, że
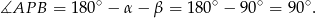
Zatem trójkąt 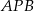 jest prostokątny. Z twierdzenia Pitagorasa mamy
jest prostokątny. Z twierdzenia Pitagorasa mamy
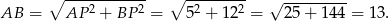
Teraz już łatwo obliczyć obwód
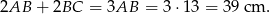
Odpowiedź: