/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7590224

Dodaj do ulubionych
Dodaj do rozwiązanych

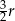Na okręgu o promieniu r opisano trapez prostokątny, którego najkrótszy bok ma długość 32r . Oblicz pole tego trapezu oraz stosunek długości jego przekątnych.

Rozwiązanie

Zaczynamy od rysunku.

PIC

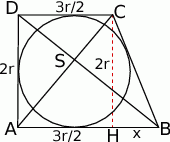
Jeżeli oznaczymy 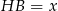HB = x , to ponieważ w czworokącie opisanym na okręgu sumy przeciwległych boków są równe, mamy

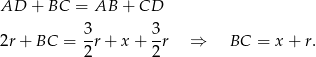
AD + BC = AB + CD 3 3 2r + BC = -r + x + --r ⇒ BC = x + r. 2 2

Napiszmy teraz twierdzenie Pitagorasa w trójkącie 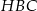HBC .

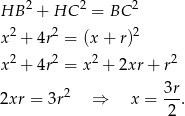
HB 2 + HC 2 = BC 2 x 2 + 4r2 = (x+ r)2 2 2 2 2 x + 4r = x + 2xr+ r 2 3r- 2xr = 3r ⇒ x = 2 .

Zatem pole trapezu jest równe

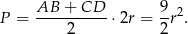
P = AB--+-CD--⋅2r = 9r2. 2 2

Długości przekątnych wyliczamy z trójkątów prostokątnych 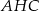AHC i ADB .

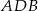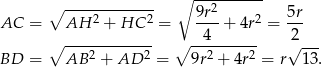
∘ ------------- ∘ ---2------ AC = AH 2 + HC 2 = 9r-+ 4r2 = 5r- ∘ ------------ ∘ --4------ 2--- BD = AB 2 + AD 2 = 9r2 + 4r2 = r√ 13.

Zatem szukany stosunek wynosi

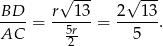
√ --- √ --- BD--= r--13-= 2--13-. AC 52r 5

 
Odpowiedź: Pole: 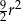9r2 2 , stosunek przekątnych: √ -- 2-513

Wersja PDF