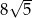/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7635648

Dodaj do ulubionych
Dodaj do rozwiązanych

W dany trapez można wpisać okrąg i jednocześnie można na tym trapezie opisać okrąg. Wysokość tego trapezu jest równa 8, a jego kąt ostry ma miarę 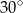30 ∘ . Oblicz długość promienia okręgu opisanego na tym trapezie.

Rozwiązanie

Szkicujemy opisaną sytuację – trapez, na którym można opisać okrąg to trapez równoramienny.

PIC

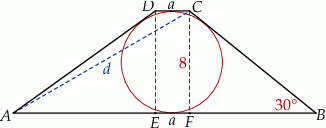
Trójkąt prostokątny 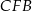CF B jest połówką trójkąta równobocznego o boku 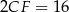2CF = 16 . Zatem 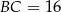BC = 16 i

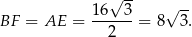
√ -- 1-6--3 √ -- BF = AE = 2 = 8 3.

Wiemy, że w trapez można wpisać okrąg, więc sumy długości przeciwległych boków są równe

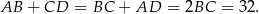
AB + CD = BC + AD = 2BC = 32.

Jeżeli więc oznaczymy 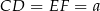CD = EF = a , to

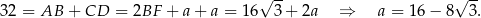
√ -- √ -- 32 = AB + CD = 2BF + a + a = 16 3 + 2a ⇒ a = 16 − 8 3 .

Możemy teraz obliczyć długość 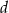d przekątnej AC .

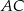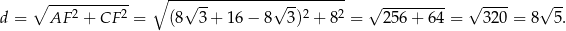
∘ ----------- ∘ --√-----------√---------- √ --------- √ ---- √ -- d = AF 2 + CF 2 = (8 3 + 16 − 8 3 )2 + 82 = 256+ 64 = 32 0 = 8 5.

Promień 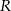R okręgu opisanego na trapezie 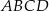ABCD jest taki sam jak promień okręgu opisanego na trójkącie 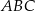ABC , więc na mocy twierdzenia sinusów

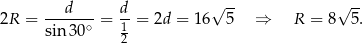
---d--- d- √ -- √ -- 2R = sin3 0∘ = 1 = 2d = 16 5 ⇒ R = 8 5. 2

 
Odpowiedź: √ -- 8 5

Wersja PDF