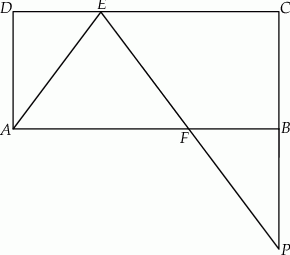
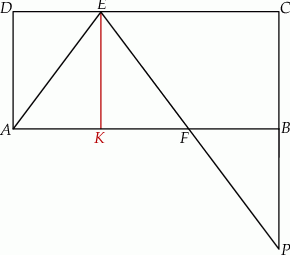
Zadanie nr 7664285
Dany jest prostokąt 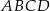 . Na boku
. Na boku 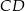 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 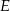 , że
, że 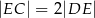 , a na boku
, a na boku 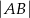 wybrano taki punkt
wybrano taki punkt 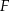 , że
, że 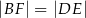 . Niech
. Niech 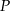 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 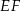 z prostą
z prostą 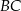 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 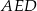 i
i 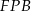 są przystające.
są przystające.
Rozwiązanie
Sposób I
Odcinek 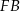 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 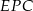 (bo
(bo 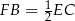 i
i 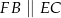 ), więc
), więc 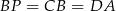 . Ponadto
. Ponadto
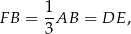
więc trójkąty prostokątne 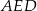 i
i 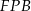 mają przyprostokątne tej samej długości. Trójkąty te są więc przystające.
mają przyprostokątne tej samej długości. Trójkąty te są więc przystające.
Sposób II
Niech 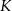 będzie środkiem odcinka
będzie środkiem odcinka 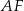 .
.
W szczególności
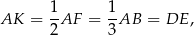
więc 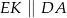 . To oznacza, że trójkąt
. To oznacza, że trójkąt 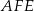 jest równoramienny (bo jego środkowa
jest równoramienny (bo jego środkowa 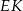 jest jednocześnie jego wysokością). W takim razie
jest jednocześnie jego wysokością). W takim razie
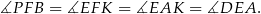
To oznacza, że trójkąty prostokątne 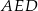 i
i 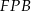 mają taki sam kąt ostry, więc są podobne. Ponadto
mają taki sam kąt ostry, więc są podobne. Ponadto 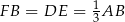 , więc są one przystające.
, więc są one przystające.

