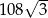Zadanie nr 7759540
Ramię trapezu równoramiennego ma długość 12 cm. Kąt ostry tego trapezu ma miarę dwa razy mniejszą niż kąt rozwarty, a przekątna trapezu jest prostopadła do ramienia. Oblicz pole trapezu.
Rozwiązanie
Szkicujemy opisaną sytuację.
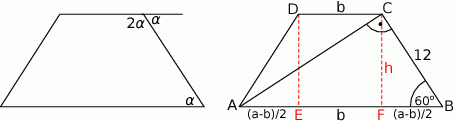
Jeżeli oznaczymy przez  kąt ostry trapezu, to kąt rozwarty trapezu ma miarę
kąt ostry trapezu, to kąt rozwarty trapezu ma miarę 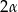 i mamy
i mamy

Oznaczmy 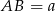 oraz
oraz 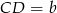 . Patrzymy teraz na trójkąt prostokątny
. Patrzymy teraz na trójkąt prostokątny 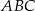 .
.
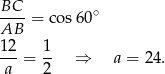
Z trójkąta prostokątnego 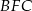 obliczamy wysokość trapezu oraz długość odcinka
obliczamy wysokość trapezu oraz długość odcinka  .
.
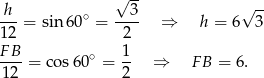
Z drugiej strony
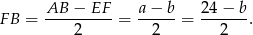
Mamy więc
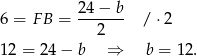
Pozostało obliczyć pole trapezu.
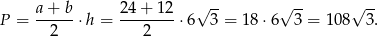
Odpowiedź: