Zadanie nr 7810207
Długości boków prostokąta 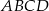 są równe:
są równe: 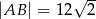 i
i 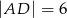 . Na odcinku
. Na odcinku 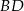 wybrano punkt
wybrano punkt 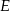 w ten sposób, że
w ten sposób, że 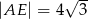 . Oblicz długość odcinka
. Oblicz długość odcinka 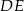 .
.
Rozwiązanie
Sposób I
Rozpoczynamy od rysunku.
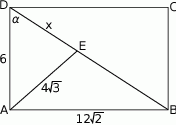
Obliczmy na początek długość przekątnej.
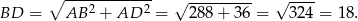
Długość odcinka 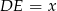 obliczymy pisząc twierdzenie cosinusów w trójkącie
obliczymy pisząc twierdzenie cosinusów w trójkącie 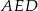 . Zanim to jednak zrobimy zauważmy, że jeżeli
. Zanim to jednak zrobimy zauważmy, że jeżeli 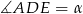 to
to
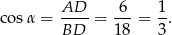
Piszemy teraz twierdzenie cosinusów w trójkącie 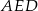 .
.
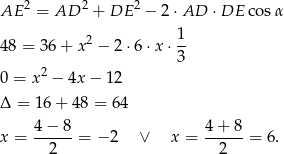
Zatem 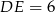 .
.
Sposób II
Umieśćmy prostokąt 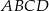 w układzie współrzędnych tak, aby
w układzie współrzędnych tak, aby 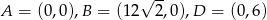 .
.
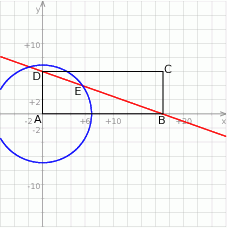
Co wiemy o punkcie 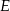 ? – wiemy, że leży jednocześnie na prostej
? – wiemy, że leży jednocześnie na prostej 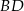 i okręgu o środku w
i okręgu o środku w 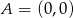 i promieniu
i promieniu 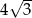 . Napiszemy więc równania prostej i okręgu i znajdziemy ich punkty wspólne.
. Napiszemy więc równania prostej i okręgu i znajdziemy ich punkty wspólne.
Z okręgiem jest łatwo:
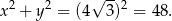
Teraz prosta 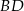 . Szukamy jej w postaci
. Szukamy jej w postaci 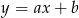 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 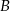 i
i 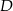 .
.
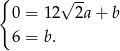
Z pierwszego równania wyliczamy 
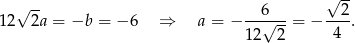
Prosta 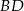 ma więc równanie
ma więc równanie 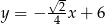 . Podstawiamy to wyrażenie do równania okręgu.
. Podstawiamy to wyrażenie do równania okręgu.
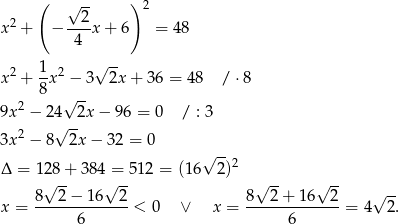
Pierwszy pierwiastek odpowiada punktowi, który nie leży na odcinku 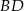 , więc
, więc 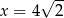 i
i
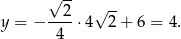
Tak więc 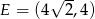 i
i
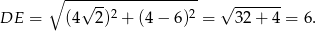
Odpowiedź: