Zadanie nr 7848321
Przekątna trapezu równoramiennego dzieli jego kąt ostry na kąty o miarach  i
i 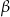 (
( – kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.
– kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.
Rozwiązanie
Zaczynamy od schematycznego rysunku.
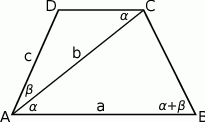
Sposób I
Zauważmy, że
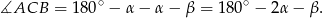
Zatem
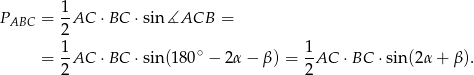
Z drugiej strony mamy
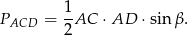
Stąd
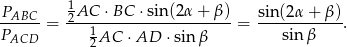
Sposób II
Ze wzoru z sinusem na pole trójkąta mamy
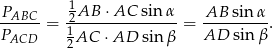
Pozostało wyliczyć stosunek 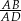 – zrobimy to korzystając z twierdzenia sinusów w trójkątach
– zrobimy to korzystając z twierdzenia sinusów w trójkątach 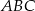 i
i 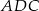 .
.
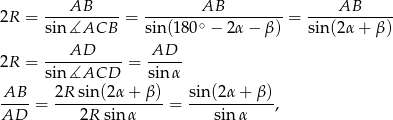
gdzie 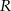 jest promieniem okręgu opisanego na trapezie
jest promieniem okręgu opisanego na trapezie 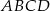 (a więc również na każdym z trójkątów
(a więc również na każdym z trójkątów 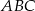 i
i 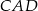 ). Mamy zatem
). Mamy zatem
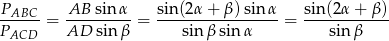
Sposób III
Poprzednie rozwiązanie można odrobinę skrócić, jeżeli skorzysta się z bardziej wyspecjalizowanego wzoru na pole trójkąta, np.
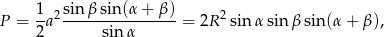
gdzie wszystkie literki mają standardowe znaczenie.
Powiedzmy, że skorzystamy z drugiego wzoru. Jak już wcześniej zauważyliśmy, promienie okręgów opisanych na trójkątach 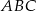 i
i 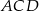 są równe (bo są równe promieniowi okręgu opisanego na całym trapezie). Zatem
są równe (bo są równe promieniowi okręgu opisanego na całym trapezie). Zatem
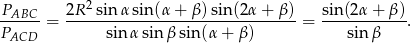
Odpowiedź: