/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7905138

Dodaj do ulubionych
Dodaj do rozwiązanych

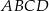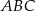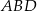Oblicz pole rombu ABCD , wiedząc, że długości promieni okręgów opisanych na trójkątach ABC i ABD odpowiednio są równe 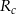Rc i Rd .

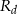Rozwiązanie

Zacznijmy od rysunku i oznaczmy 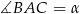∡BAC = α oraz boki rombu przez a .

PIC

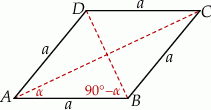
Ponieważ przekątne rombu są prostopadłe, 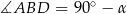∡ABD = 90∘ − α . Stosujemy twierdzenie sinusów do trójkątów 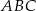ABC i ABD .

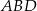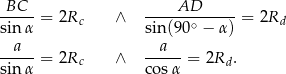
-BC-- = 2R ∧ -----AD------= 2R sin α c sin(90 ∘ − α ) d a a ----- = 2Rc ∧ ----- = 2Rd. sin α co sα

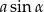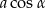Zanim będziemy to przekształcać dalej, zastanówmy się co mamy obliczyć. Pole rombu to suma czterech pól trójkątów prostokątnych. Przyprostokątne tych trójkątów mają długości boków asinα i acos α (łatwo to zobaczyć w trójkącie z podstawą 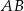AB ). Zatem pole rombu jest równe

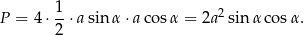
P = 4⋅ 1⋅ asinα ⋅a cosα = 2a2sin αco sα. 2

Widać zatem, że potrzebujemy z otrzymanych wcześniej zależności obliczyć 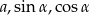a,sin α,cos α . Dzieląc te równości stronami (żeby skrócić a ) mamy

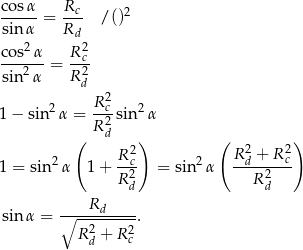
cos α Rc ----- = --- /()2 sin α Rd cos2-α -R2c 2 = R 2 sin α d 2 R2c- 2 1− sin α = R2 sin α ( d ) ( ) R 2 R 2+ R 2c 1 = sin2α 1 + --c2 = sin2α --d-2--- R d Rd Rd sin α = ∘----------. R2d + R 2c

Stąd

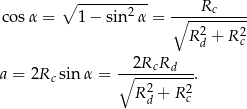
∘ -------2-- ---Rc------ cos α = 1− sin α = ∘ -------- R2d + R 2c 2R R a = 2Rc sinα = ∘----c-d---. R 2 + R 2 d c

Szukane pole wynosi zatem

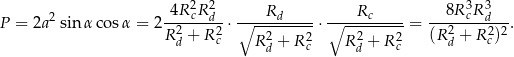
2 2 3 3 P = 2a2 sin α cosα = 2-4R-cRd- ⋅∘---Rd-----⋅ ∘---Rc-----= --8R-cRd---. R 2d + R2c R2 + R 2 R 2+ R 2 (R2d + R 2c)2 d c d c

 
Odpowiedź: --8R3cR3d- (R2d+R 2c)2

Wersja PDF