/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7909551

Dodaj do ulubionych
Dodaj do rozwiązanych

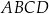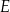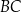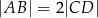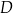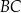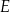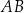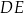W trapezie ABCD punkt E jest środkiem boku BC oraz |AB | = 2|CD | . Z wierzchołka D poprowadzono prostą przecinającą bok BC w punkcie E . Proste AB i DE przecinają się w punkcie 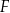F (zobacz rysunek).

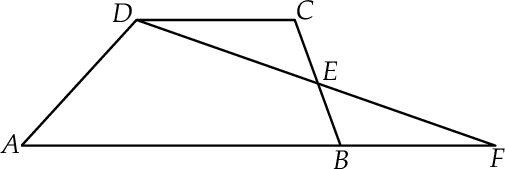
ZINFO-FIGURE

Wykaż, pole trójkąta 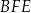BF E jest pięć razy mniejsze od pola czworokąta ABED .

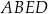Rozwiązanie

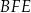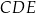Zauważmy, że trójkąty BF E i CDE mają równe kąty

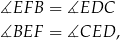
∡EF B = ∡EDC ∡BEF = ∡CED ,

więc są podobne. Ponadto, z założenia 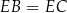EB = EC , więc trójkąty te są przystające.

Sposób I

Ustaliliśmy, że

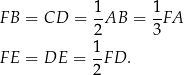
1- 1- F B = CD = 2 AB = 3 FA 1 F E = DE = --FD . 2

Na mocy wzoru na pole z sinusem, mamy

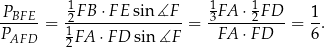
1 1 1 PBFE-- 2F-B-⋅FE-sin∡F--- -3FA-⋅2-FD- 1- PAFD = 1FA ⋅ FD sin ∡F = FA ⋅F D = 6 . 2

To oznacza, że

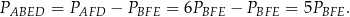
PABED = PAFD − PBFE = 6PBFE − PBFE = 5PBFE .

Sposób II

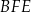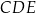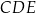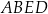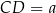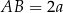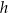Wiemy już, że trójkąty BF E i CDE są przystające, więc wystarczy obliczyć stosunek pól trójkąta CDE i czworokąta ABED . Jeżeli oznaczymy CD = a , AB = 2a i h jest wysokością trapezu ABCD , to

-PCDE-- -----PCDE------ --------12a-⋅ h2------- ---14-- --1--- 1- P = P − P = 1 1 h = 3− 1 = 6 − 1 = 5. ABED ABCD CDE 2 (a+ 2a )⋅h − 2 a⋅ 2 2 4
Wersja PDF