Zadanie nr 8088802
W trapez prostokątny 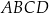 wpisano okrąg, przy czym punkt
wpisano okrąg, przy czym punkt 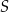 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 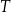 jest punktem styczności okręgu wpisanego z dłuższym ramieniem
jest punktem styczności okręgu wpisanego z dłuższym ramieniem 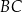 . Oblicz pole tego trapezu, jeśli
. Oblicz pole tego trapezu, jeśli 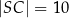 i
i 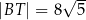 .
.

Rozwiązanie
Dorysujmy odcinki łączące punkt 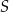 z punktami styczności z podstawami trapezu, oraz odcinek
z punktami styczności z podstawami trapezu, oraz odcinek 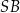 .
.
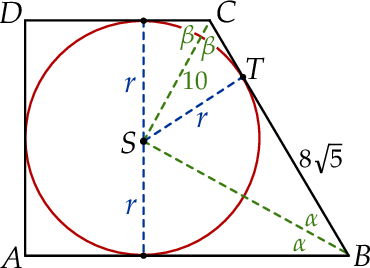
Zauważmy, że trójkąty prostokątne, których jeden bok jest promieniem okręgu wpisanego, a przeciwprostokątną jest 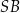 , są przystające. Zatem prosta
, są przystające. Zatem prosta 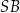 jest dwusieczną kąta
jest dwusieczną kąta 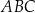 . Oznaczmy kąty na jakie dzieli ona kąt
. Oznaczmy kąty na jakie dzieli ona kąt 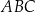 przez
przez  . Podobnie niech
. Podobnie niech 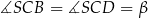 . Z równoległości prostych
. Z równoległości prostych 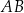 i
i 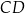 mamy
mamy
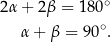
Oznacza to, że trójkąt 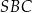 jest prostokątny. Prostokątny jest też trójkąt
jest prostokątny. Prostokątny jest też trójkąt 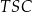 i jest on podobny do trójkąta
i jest on podobny do trójkąta 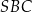 . Jeżeli oznaczymy
. Jeżeli oznaczymy 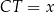 to z tego podobieństwa mamy
to z tego podobieństwa mamy
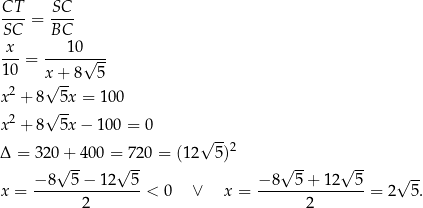
Zatem 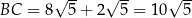 i na mocy twierdzenia Pitagorasa
i na mocy twierdzenia Pitagorasa
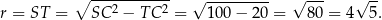
To oznacza, że wiemy jaka jest długość wysokości trapezu
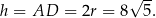
Teraz korzystamy z tego, że w czworokącie opisanym na okręgu sumy długości przeciwległych boków są równe. Zatem
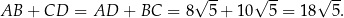
Zatem pole jest równe
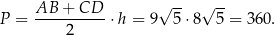
Odpowiedź: 360

