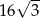/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8152914

Dodaj do ulubionych
Dodaj do rozwiązanych

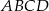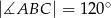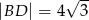W czworokącie ABCD o obwodzie 24 dane są ∘ |∡ABC | = 120 oraz √ -- |BD | = 4 3 . Wiedząc, że środek przekątnej 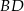BD jest środkiem symetrii tego czworokąta oblicz jego pole.

Rozwiązanie

Zaczynamy naturalnie od szkicowego rysunku.

PIC

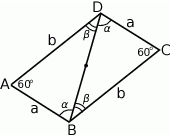
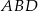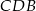Informacja o środku symetrii czworokąta oznacza, że trójkąty ABD i CDB są przystające. Jeżeli oznaczmy ich boki jak na obrazku to z podanego obwodu mamy

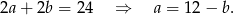
2a + 2b = 2 4 ⇒ a = 12 − b.

Ponadto wiemy, że

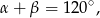
α + β = 120∘,

czyli

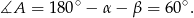
∡A = 1 80∘ − α− β = 60 ∘.

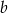Aby wyliczyć a i b napiszemy teraz twierdzenie cosinusów w trójkącie ABD .

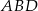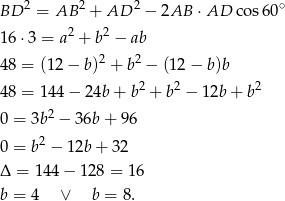
2 2 2 ∘ BD = AB + AD − 2AB ⋅ AD cos60 1 6⋅3 = a2 + b 2 − ab 2 2 4 8 = (12 − b) + b − (12− b)b 4 8 = 144 − 24b + b2 + b2 − 12b + b2 0 = 3b2 − 36b + 96 2 0 = b − 12b+ 32 Δ = 144 − 1 28 = 16 b = 4 ∨ b = 8.

Zatem 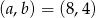(a,b) = (8,4) lub odwrotnie.

Pozostało policzyć pole czworokąta. Liczymy je ze wzoru z sinusem

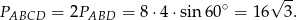
√ -- PABCD = 2PABD = 8⋅ 4⋅sin 60∘ = 16 3.

 
Odpowiedź: √ -- 16 3

Wersja PDF