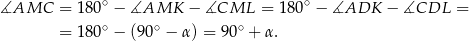/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8222896

Dodaj do ulubionych
Dodaj do rozwiązanych

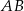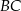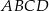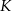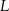Na bokach AB i BC prostokąta ABCD wybrano punkty K i L w ten sposób, że trójkąt 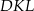DKL jest ostrokątny oraz 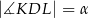|∡KDL | = α . Odcinek 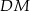DM jest wysokością trójkąta DKL .

PIC

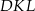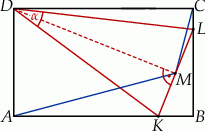
Wykaż, że 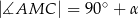|∡AMC | = 90 ∘ + α .

Rozwiązanie

Zauważmy, że punkty 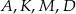A ,K ,M ,D leżą na jednym okręgu – jest to okrąg o średnicy 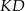KD . Analogicznie, punkty 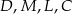D ,M ,L,C leżą na okręgu o średnicy 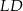LD . Kąty wpisane oparte na tym samym łuku są równe, więc

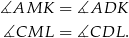
∡AMK = ∡ADK ∡CML = ∡CDL .

Stąd

∡AMC = 18 0∘ − ∡AMK − ∡CML = 180∘ − ∡ADK − ∡CDL = ∘ ∘ ∘ = 18 0 − (90 − α) = 90 + α.
Wersja PDF