/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8259897

Dodaj do ulubionych
Dodaj do rozwiązanych

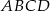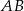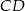Trapez prostokątny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r .

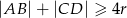  • Wykaż, że |AB |+ |CD | ≥ 4r .
  • Wiedząc, że pole trapezu jest równe 4 wykaż, że r ≤ 1 .

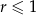Rozwiązanie

Rozpoczynamy od rysunku.

PIC

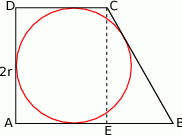
  • Ponieważ trapez jest opisany na okręgu, sumy długości jego przeciwległych boków muszą być równe, czyli
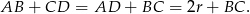
    AB + CD = AD + BC = 2r + BC .

    Wystarczy zatem pokazać, że 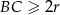BC ≥ 2r . To jednak staje się jasne jeżeli popatrzymy na trójkąt prostokątny 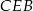CEB – przeciwprostokątna jest zawsze najdłuższym bokiem w trójkącie prostokątnym, czyli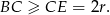

    BC ≥ CE = 2r .
  • Korzystając ze wzoru na pole trapezu oraz z nierówności z poprzedniego podpunktu, mamy
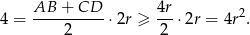
    4 = AB--+-CD--⋅2r ≥ 4r-⋅2r = 4r2. 2 2

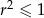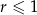    Stąd r2 ≤ 1 , czyli r ≤ 1 .

Wersja PDF