/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8359090

Dodaj do ulubionych
Dodaj do rozwiązanych

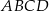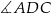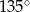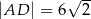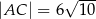Dany jest równoległobok ABCD , w którym kąt rozwarty ∡ADC ma miarę 13 5∘ . Ponadto wiadomo, że √ -- |AD | = 6 2 i √ --- |AC | = 6 1 0 (zobacz rysunek). Oblicz obwód tego równoległoboku.

PIC

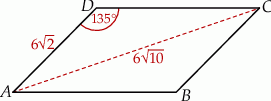
Rozwiązanie

Sposób I

Dorysujmy wysokość 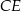CE opuszczoną z wierzchołka 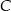C na prostą AB .

PIC

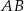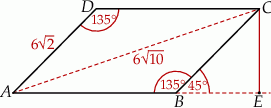
Trójkąt 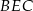BEC jest połówką kwadratu (tzn. jest to równoramienny trójkąt prostokątny), więc

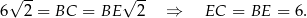
√ -- √ -- 6 2 = BC = BE 2 ⇒ EC = BE = 6 .

Z twierdzenia Pitagorasa w trójkącie 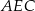AEC mamy

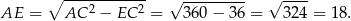
∘ ------------ √ --------- √ ---- AE = AC 2 − EC 2 = 360 − 36 = 324 = 18 .

Stąd

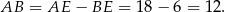
AB = AE − BE = 18 − 6 = 12.

Obwód równoległoboku jest więc równy

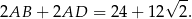
√ -- 2AB + 2AD = 24 + 12 2 .

Sposób II

Jeżeli oznaczymy 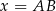x = AB , to na mocy twierdzenia cosinusów mamy

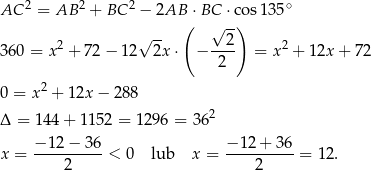
2 2 2 ∘ AC = AB + BC − 2AB( ⋅BC ⋅-c)os13 5 √ -- √ 2 3 60 = x2 + 72 − 12 2x ⋅ − ---- = x2 + 12x + 72 2 2 0 = x + 12x − 288 Δ = 144 + 1 152 = 129 6 = 362 x = −-12-−-36-< 0 lub x = −-12-+-3-6 = 12. 2 2

Zatem 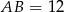AB = 1 2 i obwód równoległoboku jest równy

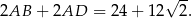
√ -- 2AB + 2AD = 24 + 12 2 .

 
Odpowiedź: √ -- 24 + 12 2

Wersja PDF