/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8545863

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie równoramiennym stosunek długości podstaw jest równy 3:4, a przekątna trapezu dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego pole jest równe 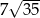√ --- 7 35 .

Rozwiązanie

Oznaczmy długości podstaw trapezu przez 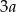3a i 4a .

PIC

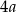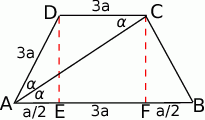
Ponieważ

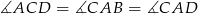
∡ACD = ∡CAB = ∡CAD

(prosta 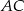AC jest dwusieczną kąta 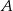A ), to trójkąt 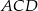ACD jest równoramienny, czyli 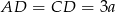AD = CD = 3a . Mamy więc

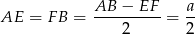
AE = FB = AB--−-EF--= a- 2 2

i stosując twierdzenie Pitagorasa w trójkącie 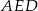AED mamy

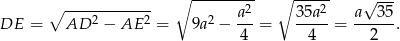
∘ ------------ ∘ --------- ∘ ----- √ --- DE = AD 2 − AE 2 = 9a2 − a2-= 35a2-= a--35-. 4 4 2

Zatem z podanego pola mamy równanie

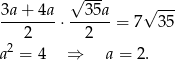
√ --- 3a-+-4a- --35a- √ --- 2 ⋅ 2 = 7 35 2 a = 4 ⇒ a = 2.

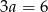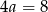Podstawy trapezy mają więc długości 3a = 6 i 4a = 8 , a ramiona mają długość 3a = 6 .  
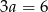Odpowiedź: 6, 6, 6, 8

Wersja PDF