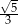/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8658074

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku boki mają długości 3 i 7, a jedna z przekątnych ma długość 6. Oblicz cosinus kąta ostrego pod jakim przecinają się przekątne tego równoległoboku.

Rozwiązanie

Szkicujemy równoległobok.

PIC

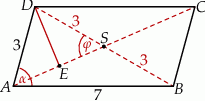
Spróbujemy obliczyć długość drugiej przekątnej równoległoboku. Aby móc to zrobić, obliczmy najpierw cosinus kąta 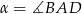α = ∡BAD . W tym celu piszemy twierdzenie cosinusów w trójkącie ABD .

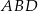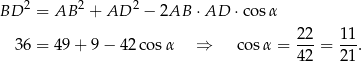
BD 2 = AB 2 + AD 2 − 2AB ⋅AD ⋅c osα 36 = 49+ 9− 42cos α ⇒ cosα = 22-= 11. 42 21

To oznacza, że

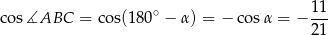
11 co s∡ABC = cos(180∘ − α) = − cos α = − --- 21

i

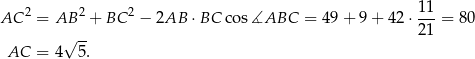
2 2 2 11 AC = AB + BC − 2AB ⋅BC cos ∡ABC = 49+ 9+ 42⋅ ---= 8 0 √ -- 21 AC = 4 5.

Cosinus kąta 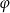φ między przekątnymi obliczymy na dwa sposoby.

Sposób I

Trójkąt 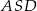ASD jest równoramienny. Niech 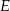E będzie środkiem jego podstawy. Mamy zatem

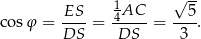
√ -- ES 14AC 5 cos φ = ----= ----- = ---. DS DS 3

Sposób II

Piszemy twierdzenie cosinusów w trójkącie 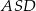ASD .

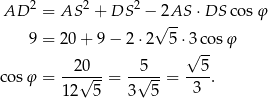
AD 2 = AS 2 + DS 2 − 2AS ⋅ DS co sφ √ -- 9 = 20 + 9 − 2⋅ 2 5⋅√3cos φ 20 5 5 cosφ = --√---= -√---= ----. 12 5 3 5 3

 
Odpowiedź: √ - -35

Wersja PDF