Zadanie nr 8658883
Trapez 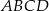 (
(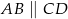 ,
, 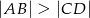 ) jest wpisany w okrąg o promieniu długości
) jest wpisany w okrąg o promieniu długości 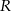 . Wiadomo że kąt ostry trapezu ma miarę
. Wiadomo że kąt ostry trapezu ma miarę  zaś
zaś 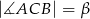 , gdzie
, gdzie 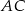 jest przekątną trapezu. Oblicz długość
jest przekątną trapezu. Oblicz długość  dłuższej podstawy tego trapezu oraz długość
dłuższej podstawy tego trapezu oraz długość 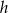 jego wysokości.
jego wysokości.
Rozwiązanie
Zaczynamy od rysunku.
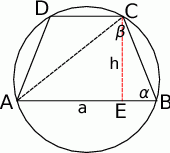
Na mocy twierdzenia sinusów w trójkącie 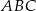 mamy
mamy
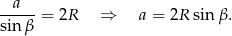
W tym samym trójkącie mamy
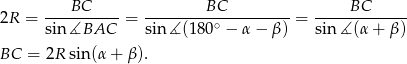
Patrzymy teraz na trójkąt prostokątny 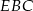 .
.
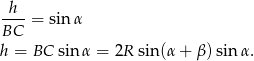
Odpowiedź: 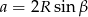 ,
,