Zadanie nr 8697280
Dany jest czworokąt 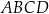 . Niech
. Niech 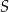 będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt
będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt 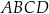 można wpisać w okrąg wtedy i tylko wtedy, gdy
można wpisać w okrąg wtedy i tylko wtedy, gdy 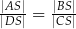 .
.
Rozwiązanie
Szkicujemy czworokąt wpisany w okrąg.
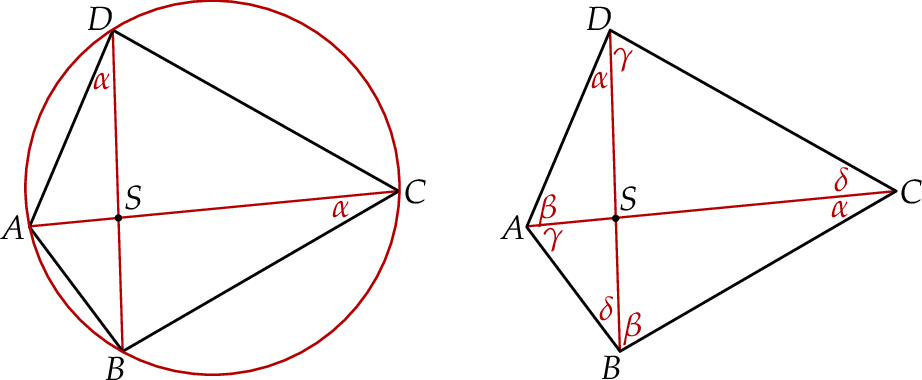
Twierdzenie, które mamy udowodnić ma formę równoważności, więc musimy wykazać dwie implikacje.
„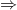 ”
”
Jeżeli czworokąt 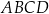 jest wpisany w okrąg, to na mocy twierdzenia o równości kątów wpisanych mamy
jest wpisany w okrąg, to na mocy twierdzenia o równości kątów wpisanych mamy
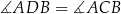
To oznacza, że trójkąty 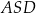 i
i 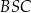 mają dwa równe kąty (drugi równy kąt to ten przy wierzchołku
mają dwa równe kąty (drugi równy kąt to ten przy wierzchołku 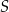 ). To oznacza, że trójkąty te są podobne, czyli
). To oznacza, że trójkąty te są podobne, czyli
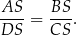
„ ”
”
Odwrotnie, z równości
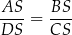
wynika, że trójkąty 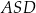 i
i 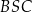 są podobne (bo mają wspólny kąt przy wierzchołku
są podobne (bo mają wspólny kąt przy wierzchołku 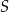 ). Analogicznie, jeżeli zapiszemy powyższy warunek w postaci
). Analogicznie, jeżeli zapiszemy powyższy warunek w postaci
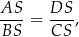
to widać, że podobne też są trójkąty 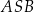 i
i 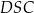 . Z powyższych podobieństw mamy
. Z powyższych podobieństw mamy
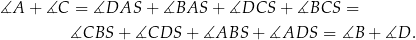
To oznacza, że w czworokącie 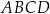 sumy przeciwległych kątów są równe, więc na czworokącie tym można opisać okrąg.
sumy przeciwległych kątów są równe, więc na czworokącie tym można opisać okrąg.

