/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8836981

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawy trapezu równoramiennego mają długości 3 i 5, a jego ramię ma długość 2. Oblicz promień okręgu opisanego na tym trapezie.

Rozwiązanie

Zaczynamy od rysunku.

PIC

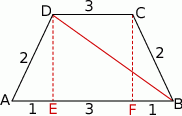
Okrąg opisany na trapezie to ten sam okrąg, co okrąg opisany na trójkącie 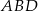ABD . Możemy więc wyliczyć jego promień z twierdzenia sinusów. Aby móc to zrobić musimy wyliczyć długość przekątnej 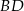BD oraz sinus kąta 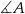∡A . Zacznijmy od wyliczenia wysokości 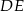DE – patrzymy na trójkąt prostokątny AED .

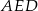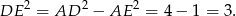
2 2 2 DE = AD − AE = 4 − 1 = 3 .

Teraz liczymy długość przekątnej (patrzymy na trójkąt prostokątny 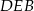DEB ).

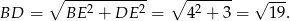
∘ ------------ ∘ ------- √ --- BD = BE 2 + DE 2 = 42 + 3 = 19.

Mamy ponadto

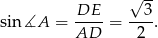
√ -- sin∡A = -DE- = --3. AD 2

Teraz korzystamy z twierdzenia sinusów w trójkącie 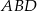ABD .

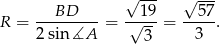
√ --- √ --- --BD----- --19- --57- R = 2sin ∡A = √ 3 = 3 .

 
Odpowiedź: √ -- --57 3

Wersja PDF