Zadanie nr 8905110
W prostokącie 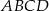 połączono wierzchołki
połączono wierzchołki 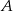 i
i 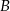 ze środkiem boku
ze środkiem boku 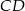 i otrzymano trójkąt, którego jeden z kątów ma miarę
i otrzymano trójkąt, którego jeden z kątów ma miarę 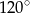 . Wiedząc, że
. Wiedząc, że 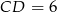 oblicz obwód prostokąta
oblicz obwód prostokąta 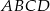 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
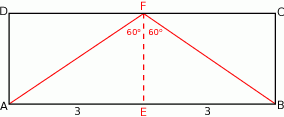
Kąty przy podstawie trójkąta równoramiennego 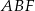 są na pewno ostre (mniejsze od
są na pewno ostre (mniejsze od 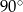 ) co oznacza, że
) co oznacza, że 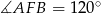 . Jeżeli poprowadzimy wysokość
. Jeżeli poprowadzimy wysokość 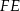 w trójkącie
w trójkącie 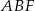 to mamy
to mamy
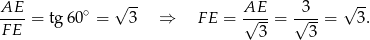
Zatem obwód prostokąta 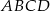 jest równy
jest równy
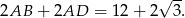
Odpowiedź: