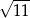/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 8927729

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku, w którym boki mają długości 1 i 3, symetralna krótszego boku przechodzi przez wierzchołek równoległoboku. Znajdź długości przekątnych tego równoległoboku.

Rozwiązanie

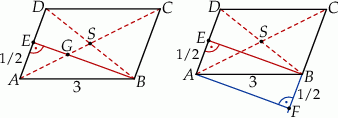
Zaczynamy od rysunku

PIC

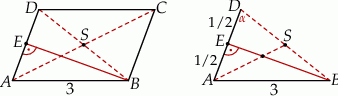
Odcinek 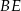BE jest jednocześnie wysokością i symetralną boku 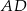AD trójkąta 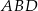ABD . Oznacza to, że trójkąt ten jest równoramienny. Zatem 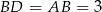BD = AB = 3 . Długość drugiej przekątnej wyliczymy na dwa sposoby.

Sposób I

Jak się dobrze przyjrzeć, to wszystkie interesujące nas odcinki są w trójkącie 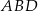ABD i możemy się na nim skoncentrować. Tak naprawdę musimy wyliczyć długość jego środkowej 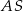AS (przekątna 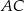AC jest dwa razy dłuższa). Zrobimy to stosując twierdzenie cosinusów w trójkącie 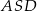ASD , ale najpierw wyliczymy cosα .

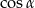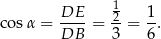
1 cosα = DE--= 2-= 1-. DB 3 6

Pozostało zastosować twierdzenie cosinusów.

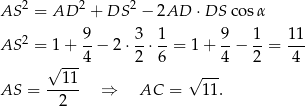
2 2 2 AS = AD + DS − 2AD ⋅DS cosα 2 9- 3- 1- 9- 1- 11- AS = 1 + 4 − 2 ⋅2 ⋅ 6 = 1 + 4 − 2 = 4 √ --- √ --- AS = --1-1 ⇒ AC = 11. 2

Sposób II

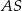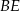Zauważmy, że odcinki AS i BE są środkowymi w trójkącie ABD .

PIC

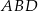Wiemy, że środkowe dzielą się w stosunku 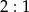2 : 1 , więc jeżeli 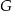G jest ich punktem wspólnym to

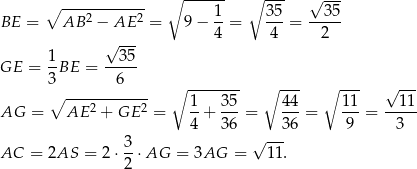
∘ ------ ∘ --- --- ∘ ------------ 1 35 √ 35 BE = AB 2 − AE 2 = 9− --= ---= ----- √ --- 4 4 2 1 35 GE = 3BE = -6--- ∘ ------------ ∘ -------- ∘ --- ∘ --- √ --- AG = AE 2 + GE 2 = 1-+ 35-= 44-= 11-= --11- 4 36 36 9 3 3 √ --- AC = 2AS = 2 ⋅--⋅AG = 3AG = 11. 2

Sposób III

Tym razem dorysujmy wysokość 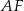AF równoległoboku opuszczoną z wierzchołka A .

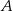Mamy zatem trójkąt prostokątny 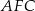AF C – z niego wyliczymy długość przekątnej 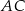AC . Mamy

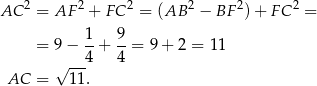
2 2 2 2 2 2 AC = AF + FC = (AB − BF )+ F C = 1- 9- = 9− 4 + 4 = 9+ 2 = 11 √ --- AC = 11.

 
Odpowiedź: 3 i √ --- 11

Wersja PDF