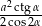Zadanie nr 8982359
W trapezie 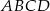 boki nierównoległe
boki nierównoległe 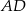 i
i 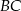 zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane
zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane 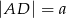 oraz
oraz 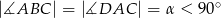 .
.
Rozwiązanie
Zacznijmy od rysunku.
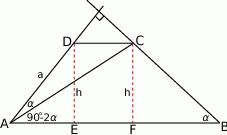
Ponieważ 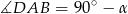 , mamy
, mamy
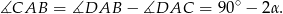
Na rysunku mamy sporo trójkątów prostokątnych, z których powyliczamy długości wysokości oraz podstaw trapezu.
Sposób I
Z trójkąta 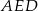 mamy
mamy
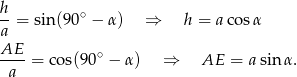
Teraz patrzymy na trójkąt 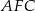 .
.
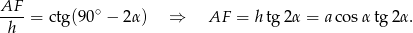
Zatem
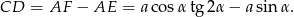
Teraz patrzymy na trójkąt 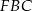 .
.
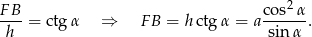
Zatem pole jest równe
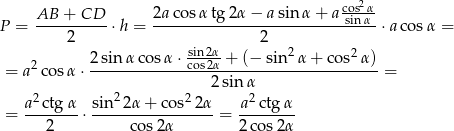
Sposób II
Podobnie jak poprzednio wyliczamy
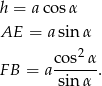
To co zrobimy inaczej, to wyliczymy długość odcinka 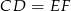 bezpośrednio z twierdzenia sinusów w trójkącie
bezpośrednio z twierdzenia sinusów w trójkącie 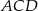 . Aby to zrobić zauważmy, że
. Aby to zrobić zauważmy, że 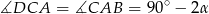 . Zatem
. Zatem
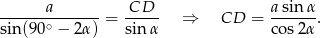
Zatem pole jest równe
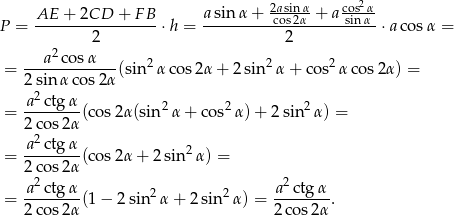
Sposób III
Tym razem pójdziemy jeszcze dalej, i obie podstawy wyliczymy z twierdzenia sinusów. Podobnie jak poprzednio wyliczamy
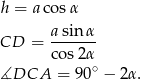
Aby wyliczyć podstawę 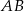 , skorzystamy z twierdzenia sinusów w trójkącie
, skorzystamy z twierdzenia sinusów w trójkącie 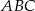 . Zanim to zrobimy popatrzmy na trójkąt
. Zanim to zrobimy popatrzmy na trójkąt 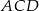 .
.
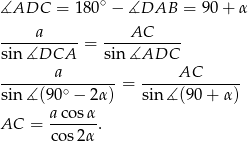
Ponieważ 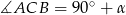 , patrząc na trójkąt
, patrząc na trójkąt 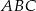 mamy
mamy
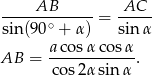
Zatem pole jest równe
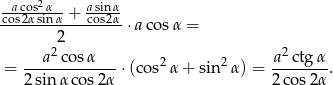
Odpowiedź: