Zadanie nr 9097307

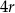Na okręgu o promieniu opisano trapez równoramienny, którego długość jednej z podstaw wynosi . Oblicz odległość środka okręgu od wierzchołków trapezu.

Rozwiązanie

Zacznijmy od szkicowego rysunku.

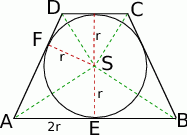
Długość odcinka 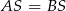AS = BS łatwo wyliczamy z trójkąta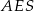 AES

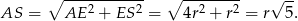
∘ ----------- ∘ -------- √ -- AS = AE 2 + ES 2 = 4r2 + r2 = r 5.

Aby wyliczyć długość odcinka 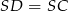SD = SC , zauważmy, że

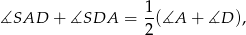
∡SAD + ∡SDA = 1(∡A + ∡D ), 2

czyli trójkąt 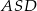ASD jest prostokątny. Ponadto trójkąt 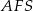AF S jest do niego podobny (bo też jest prostokątny i mają wspólny kąt ostry). Mamy zatem

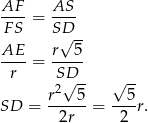
AF--= AS-- F S SD√ -- AE r 5 ----= ----- r SD√ -- √ -- r2--5- --5- SD = 2r = 2 r.

Odpowiedź: 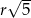√ -- r 5 i √ - --5r 2

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz