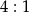Zadanie nr 9157143
W trapez równoramienny, który nie jest równoległobokiem, wpisano okrąg promieniu 4 cm. Ramię trapezu ma długość 10 cm. Punkty styczności okręgu z ramionami trapezu dzielą obwód trapezu na dwie częsci. Oblicz stosunek długości tych części.
Rozwiązanie
Zaczynamy od rysunku.
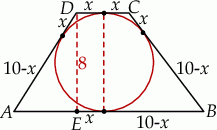
Jeżeli oznaczymy odległości punktów 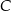 i
i 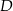 od punktów styczności z okręgiem przez
od punktów styczności z okręgiem przez  , to odległości punktów
, to odległości punktów 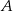 i
i 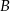 od punktów styczności z okręgiem są równe
od punktów styczności z okręgiem są równe 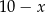 . Patrząc na trójkąt prostokątny
. Patrząc na trójkąt prostokątny 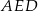 mamy
mamy
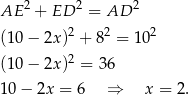
Zatem szukany stosunek wynosi
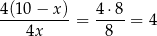
Odpowiedź: