/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 9177591

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole trapezu równoramiennego opisanego na okręgu jest równe 80, a cosinus kąta rozwartego tego trapezu jest równy 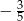− 35 . Oblicz długość ramienia tego trapezu.

Rozwiązanie

Zaczynamy od rysunku.

PIC

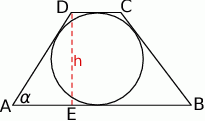
Obliczmy sinus kąta ostrego trapezu.

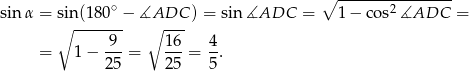
∘ ---------------- sinα = sin (180∘ − ∡ADC ) = sin∡ADC = 1 − cos2∡ADC = ∘ ------- ∘ --- = 1 − -9-= 1-6 = 4-. 25 2 5 5

Sposób I

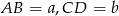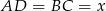Oznaczmy AB = a,CD = b i AD = BC = x . Obliczamy pole trapezu 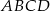ABCD jako sumę pól trójkątów 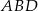ABD i BDC .

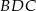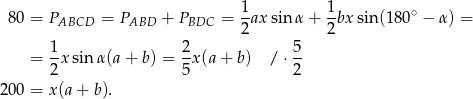
1 1 80 = PABCD = PABD + PBDC = --ax sin α + --bxsin(18 0∘ − α) = 2 2 = 1-xsin α(a + b) = 2-x(a + b) / ⋅ 5- 2 5 2 200 = x(a + b).

Korzystamy teraz z tego, że 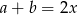a + b = 2x (bo trapez jest opisany na okręgu). Mamy więc

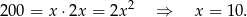
200 = x⋅ 2x = 2x2 ⇒ x = 10.

Sposób II

Niech 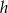h oznacza wysokość trapezu. Z trójkąta prostokątnego 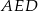AED mamy

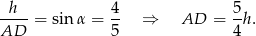
-h-- 4- 5- AD = sin α = 5 ⇒ AD = 4 h.

Korzystamy teraz z tego, że 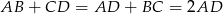AB + CD = AD + BC = 2AD (bo trapez jest opisany na okręgu). Mamy zatem

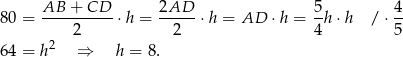
AB + CD 2AD 5 4 8 0 = ----2-----⋅ h = --2-- ⋅h = AD ⋅ h = 4-h⋅h / ⋅5- 2 6 4 = h ⇒ h = 8.

Stąd

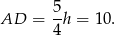
AD = 5-h = 10. 4

 
Odpowiedź: 10

Wersja PDF